It's based on the recursive relation that
1/2 = 1/3 + (1/3)*(1/2)
(and division by 3 is achievable by shifting)
So, to divide some number ABCD, you do the following
Code: Select all
A B C D / 2
-----------
A B C . D
A B . C D
+ A . B C D
-----------------
[0, A, A+B, A+B+C].[B + C + D, C+D, D]
Code: Select all
void bw_bisect(word target) {
register int i;
register int tmp = 0, sum = 0;
register int residual = 0;
register int power = 1;
for(i = 0; i < WORD_DIGITS-1; i++, power*=3) {
tmp += target[i];
residual += power * tmp;
}
for(i = WORD_DIGITS-1; i >= 0; i--) {
tmp = target[i];
target[i] = sum;
sum += tmp;
}
if(residual > 0) {
target[0] += (residual + (NBWORD_MAX/3)/2) / (NBWORD_MAX/3);
} else {
target[0] += (residual - (NBWORD_MAX/3)/2) / (NBWORD_MAX/3);
}
bw_ripple(target);
}
/* Helper function. "smears" out a number so that
* individual digits hold numbers that are in the
* range -1,...,1 */
int bw_ripple(word target) {
register int i;
register int carry = 0;
for(i = 0; i < WORD_DIGITS; i++) {
target[i] += carry;
if(target[i] > 0)
carry = (target[i] + 1) / 3;
else
carry = (target[i] - 1) / 3;
target[i] -= 3 * carry;
}
return carry;
}

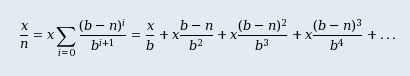
 where |q|<1
where |q|<1
