предлагаю определиться по всем типам данных и по целочисленным в т.ч.
(вероятнее всего это уже рассматривалось и обсуждалось - здесь я предлагаю это систематизировать)
предлагаю следующие варианты:
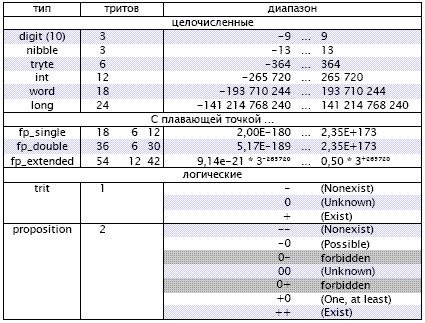
все типы предлагаю использовать знаковые (!) для представления сравнимого по мощности двоичного числа необходимо почти втрое большее троичное что позволяет той же разрядность перкрыть диапазон беззнакового представления числа в существующей 2ной системе представления так и такой же диапазон отрицательных чисел.
ЦЕЛОЧИСЛЕННЫЕ:
1. тип Digit - для поддержки 3-10ной арифметики наиболее очевидно применение - калькуляторы, что представляется одним и наиболе вероятных первых коммерческих применний 3ного МК.
2. тип Nibble - логичное расширение типа Digit для использования всей мощности представления числа 3мя разрядами.
3. тип Tryte - размер основной рабочей единицы информации должен перекрывать диапазон представления существующей 2ной системы (байт)
4. тип Int - размер должен покрывать Int существующего 2ного представления (вообще-то это 11 разрядов но для удобства предлагется использовать числа кратные трайтам)
5. тип Word - предполагется что этот тип будет равен машинному слову. на мой взгляд естественным представляется использование для машинного слова 3 трайт (учитывая что и изменение адреса так же будет производиться в 3ной системе счисления то логичным представляется следующем шагом после трайта иметь машинное слово 3 трайта)
6. тип Long - так же для покрытия диапазона Long существующего 2ного.
С ПЛАВАЮЩЕЙ ТОЧКОЙ:
fp_Single - базовый тип представления чисел с плавающей точкой.
не вижу необходимости использования отдельного разряда для обозначения знака числа и скрытого разряда как в 2ном представлении, посему представляется целесообразным отказаться от прямого следования стандарту представления чисел с плавающей точкой для 2ных и 2-10ных чисел (IEEE754 и IEEE854 соотв.)
для удобства работы целесообразно было бы иметь величины мантиссы и порядков кратными трайту если он удовлетворяют условию необходимой точности представления чисел.
учитывая что базовым машинным словом при котором имеет смысл представлять число с плавающей точкой является 3х-трайтное с учетом вышесказанного буду отталкиваться от разрядности 18 и представления 12 разрядов на мантиссу и 6 на порядок - соотвественно диапазон представляе5мых чисел 2,00E-180 ... 2,35E+173
на мой взгляд этот диапазон более чем достаточен для базового типа с плавающей точкой потому что к примеру число атомов на земле оценивается порядка 1,0Е+108
теперь что касается 2й точности (fp_Double) - его назначение повысить точность вычислений в основном за счет точности представления данных. двукратное повышение точности требует не менее чем 2-кратного повышения разрядности мантиссы, следовательно если брать базовый тип 6+12 разрядов то получаем что мантиса не должны быть меньше 2х12=24 разряда. учитывая что следующее по размерам машинное слово логично было представить удвоенным одинарным (т.е 2х18=36) получаем что число удвоеной точности должно быть 36 разрядным. не вижу необходимости увеличивать разрядность порядка т.к. мы уже имеем достаточно мощный диапазон представления чисел при том что значительно повышется точность, в то же время при сохранении порядка кратым 1 трайту сильно упрощает обработку таких чисел в т.ч. и програмным путем.
+ это сущестуенно упростит преобразование типов с плавающей чочкой(!) без существенной потери точности.
тип fp_Extended предназначен для проведения операций над числами с плавающей чтокой сминимизацией потерь точности за счет округления при вычислениях.
соотвесвтенно длина его мантиссы должна быть не меньше суммы длинн мантисс типов с одинарной и двойной точностями.
теперь о представляемых значениях
предлагаю следующие:
<e++..++ m++..++> +бесконечность(+OO)
<e++..++ m - -.. - -> -бесконечность(-OO)
<e00..00 m00..00> абсолютный 0
<e++..++ m00..00> не число (NAN)
<e - -.. - - m00..00> не число (NAN)
<e - -.. - - m00..0+> минимально представимое положительное (+0)
<e - -.. - - m00..0 -> минимально представимое отрицательное (-0)
<e##..## m0#..##> денормализованное число
<e##..## m##..##> нормализованное число
касательно минимально представимых - дальнейшее уменьшение не изменяет числа по сути младший разряд выполняет роль guard-разряда
ЛОГИЧЕСКИЕ ТИПЫ:
1. trit - минимальная единица информации. много не представшь
2. proposition - основной тип для реализации логики высказываний. в отлчие от значений представляемых trit-ом обладает замкнутостью относительно логических операций (результат принатдлежит тому же множеству что и аргументы).
ОКРУГЛЕНИЕ
предлагаю использовать 5 способов округления
1. round - округление к ближайшему (отбрасывание хвоста)
2. round+ - округление к +OO
3. round- - округление к -OO
4. roundU - округление к OO
5. roundZ - округление к 0
реализация округления важный момент для интервальной арифметики и операций с плавающей точкой.
round+ и round-
для целочисленных типов - приводят к округлению соотвевенно к ближайшему большему и к ближайшему меньшему целому.
для плавающей точки - эти способы округления представляются не имеющими ценности (во всяком случае я пока не вижу)
roundU и roundZ
для целочисленных типов - приводят к оруглению соотвевенно к ближайшему большему по модулю и к ближайшему меньшему по модулю целому.
для плавающей точки - соотвествнно к ближайшему большему и ближайшему меньшему представимым.
пока примерно так.
хотелось бы услышать мнения, предложения, возражения и дополнения.
желательно с описанием обоснования.
PS: кстати, ввиду того что зачастую логически операции в современном программировании используются для маскирования и других битовых операций или для ускоренного вычисления арифметичских выражений то есть прдложение отказаться от такого устройства как АЛУ в принципе и разделить операции по классам:
1. арифметические
2. операции над разрядами (туда же можно отнести и основные операции такие как логическое И и логическое ИЛИ и т.п.
и вообще класс поразрядных операций и логических функций)
3. собствено логические операции.
(основная причина выделения класса именно логических операций заключается в том что trit не позовляет выразить всю мощь многозначной логики поскольку не обладает замкнутостью хотя бы относительно функции отрицания/дополнения)

