nedoPC.org

Community for electronics hobbyists, established in 2002
FAQ
Last visit was: 08 Nov 2024 17:51
 It is currently 08 Nov 2024 17:51

Board index » NEDOPC IN RUSSIAN » Проект nedoPC

All times are UTC - 8 hours [ DST ]



 Page 4 of 5
  [ 65 posts ]  Go to page Previous  1, 2, 3, 4, 5  Next
Previous topic | Next topic 
Создаём подобие JPEG для ретрокомпов (Walsh+Huffman) 
Author Message
Shaos
Admin
User avatar

Joined: 08 Jan 2003 23:22
Posts: 23398
Location: Silicon Valley
Post Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)
Shaos wrote:
Я придумал как поддержать Q с мелким шагом от 1 до 99 :)

Просто начинаем отбрасывать отсчёты (стартуя с правого-нижнего угла спектра) -1 и +1 пока не доберёмся до нужного процента ;)
Если выкинув все -1 и +1 не добрались до нужного процента, то начинаем выкидывать -2 и +2 и т.д.
По сути квантование это и делает, только очень грубо - сразу помногу, а так мы как бы добавляем мелкую корректировку, чтобы подкрутить процент до желаемого :rotate:

Shaos wrote:
Возможно как раз от Q=99 и надо плясать (наплевав на выбор старта исходя из шага квантования и т.д.) - выбираем самую высокую битность (в данном случае 10bits/sample) и там поиск начала квантования НЕ нужен - отсчёты кодируются все как есть (кроме [0][0] который всегда отдельно). Далее отбрасываем низкие по амплитуде отсчёты для достижения нужного Q (если Q=99 то останавливаемся прямо сразу). Далее идём в следующую битность - 9bits/sample и стартуем сначала квантования 255 (в этом случае опять же Q будет 99) и двигаемся вверх, ища самую первую строку, где Q больше либо равна желаемой и начинаем отбрасывать низкие по амплитуде отсчёты там пока не достигнем желаемой Q, далее двигаемся в 8bits/sample и стартуем с уровня 127 и т.д.

Вот попробовал отбрасывать "слабые" отсчёты без квантования, пользуясь старым функционалом "фильтрование по уровню"

Отбрасываем -1 и +1 (процент ненулевых отсчётов упал до 58%):

Attachment:
walshexp_FemaleR_removed1s_x3.png

Далее ещё и -2 и +2 убираем (процент ненулевых стал 42%):

Attachment:
walshexp_FemaleR_removed1s2s_x3.png

Ну чисто для примера -3 и +3 (31% ненулевых остался - тут пожалуй уже надо квантование включать, а не просто отбрасывать):

Attachment:
walshexp_FemaleR_removed1s2s3s_x3.png


You do not have the required permissions to view the files attached to this post.

_________________
https://mastodon.social/@Shaos :dj:
https://www.youtube.com/@Shaos1973
24 Nov 2023 00:16 WWW
Shaos
Admin
User avatar

Joined: 08 Jan 2003 23:22
Posts: 23398
Location: Silicon Valley
Post Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)
Вот более полная таблица коэффициентов сжатия K, фактора качества Q и ошибки ERR в зависимости от параметров квантования картинки FEMALER.BWS:
Code:
FEMALER | 10bits/samp | 9bits/sampl | 8bits/sampl | 7bits/sampl | 6bits/sample   | 5bits/sample   |
--------+-------------+-------------+-------------+-------------+----------------+----------------+
   1826 | <<< [0][0] always stored separately in 16 bits (unsigned)           ERR|             ERR|
    388 |*K=1.27 Q=99 | K=1.51 Q=99 | K=1.98 Q=69 | K=3.15 Q=40 | K=4.84 Q=17 9% | K=8.96 Q=8     |
    346 | K=1.27 Q=99 | K=1.48 Q=99 | K=1.94 Q=69 | K=2.72 Q=49 | K=4.52 Q=22 8% | K=7.89 Q=8     |
    283 | K=1.27 Q=99 | K=1.31 Q=99 | K=1.80 Q=69 | K=2.55 Q=49 | K=4.03 Q=28 7% | K=6.78 Q=12    |
    244 | K=1.27 Q=99 |*K=1.28 Q=99 | K=1.60 Q=99 | K=2.13 Q=69 | K=3.37 Q=36 6% | K=5.96 Q=15    |
    199 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.53 Q=99 | K=2.00 Q=69 | K=3.17 Q=36 5% | K=4.90 Q=17 9% |
    157 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.40 Q=99 | K=1.88 Q=69 | K=2.66 Q=49 5% | K=4.48 Q=22 8% |
    148 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.35 Q=99 | K=1.83 Q=69 | K=2.62 Q=49 4% | K=4.10 Q=28 8% |
    145 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.33 Q=99 | K=1.82 Q=69 | K=2.57 Q=49 4% | K=4.10 Q=28 7% |
    125 | K=1.27 Q=99 | K=1.28 Q=99 |*K=1.29 Q=99 | K=1.61 Q=99 | K=2.15 Q=69 5% | K=3.97 Q=28 6% |
    124 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.29 Q=99 | K=1.60 Q=99 | K=2.15 Q=69    | K=3.38 Q=35 7% |
    123 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.29 Q=99 | K=1.60 Q=99 | K=2.15 Q=69    | K=3.37 Q=35 7% |
    119 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.29 Q=99 | K=1.60 Q=99 | K=2.14 Q=69    | K=3.37 Q=35 6% |
    112 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.29 Q=99 | K=1.59 Q=99 | K=2.11 Q=69    | K=3.29 Q=35 6% |
    109 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.29 Q=99 | K=1.58 Q=99 | K=2.11 Q=69    | K=3.28 Q=35 6% |
     97 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.29 Q=99 | K=1.52 Q=99 | K=2.00 Q=69    | K=3.17 Q=35 5% |
     92 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.28 Q=99 | K=1.51 Q=99 | K=1.99 Q=69    | K=2.76 Q=48 6% |
     87 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.28 Q=99 | K=1.49 Q=99 | K=1.96 Q=69    | K=2.75 Q=48 5% |
    ... | ...... Q=99 | ...... Q=99 | ...... Q=99 | ...... Q=99 | ...... Q=69    | ...... Q=48    |
     63 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.28 Q=99 |*K=1.29 Q=99 | K=1.61 Q=99    | K=2.52 Q=48 4% |
    ... | ...... Q=99 | ...... Q=99 | ...... Q=99 | ...... Q=99 | ...... Q=99    | .............. |
     31 | K=1.25 Q=99 | K=1.25 Q=99 | K=1.26 Q=99 | K=1.26 Q=99 |*K=1.27 Q=99 2% | K=1.55 Q=99 4% |

Notes: Diagonal traversal, Huffman only

В каждой колонке звёздочка означает точку с которой (и ниже) кодирование идёт без квантования (т.е. шаг квантования равен 1.0) - при этом качество устанавливается в 99 и отсчёты кодируются как есть без искажений (если не считать отбрасывание дробной части из-за которой ошибка ERR обычно не бывает меньше 2%), а всё что выше звёздочки будет с искажениями (даже если Q=99).

Наверное надо брать по верхней планке - скажем если пользователь заказал Q=60, то в каждой колонке ищем самую верхнюю строчку, где получающееся качество <=60 (в данном примере Q=69) и далее убираем столько -1 и +1 отсчётов, сколько потребуется, чтобы уменьшить процент ненулевых отчётов до нужного числа (60%) и далее считаем коэффициент сжатия для разных вариаций обходов матрицы и способов сжатия - выбираем тот вариант, что меньше (а если размеры получились одинаковыми для разных вариантов, то выбираем вариант с меньшей ошибкой).

По процентам наверное от 99 до 90 делаем без квантования (на уровне звёздочки в каждой колонке), от 89 до следующей перед 99 величине - в данном случае 69 - берём Q=99 по верхней планке, далее по верхней планке Q=69 и т.д. Убирать -1 и +1 чтобы подогнать итоговое качество к заказанному Q по-видимому надо с конца в соответствии с выбранной стратегией обхода матрицы, чтобы выиграть на отбрасывании хвостовых нулей (и если все отсчёты -1 и +1 исчерпались, то надо убирать -2 и +2 и т.д.).

_________________
https://mastodon.social/@Shaos :dj:
https://www.youtube.com/@Shaos1973
27 Nov 2023 20:36 WWW
Shaos
Admin
User avatar

Joined: 08 Jan 2003 23:22
Posts: 23398
Location: Silicon Valley
Post Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)
Shaos wrote:
Наверное надо брать по верхней планке - скажем если пользователь заказал Q=60, то в каждой колонке ищем самую верхнюю строчку, где получающееся качество <=60 (в данном примере Q=69) и далее убираем столько -1 и +1 отсчётов, сколько потребуется, чтобы уменьшить процент ненулевых отчётов до нужного числа (60%) и далее считаем коэффициент сжатия для разных вариаций обходов матрицы и способов сжатия - выбираем тот вариант, что меньше (а если размеры получились одинаковыми для разных вариантов, то выбираем вариант с меньшей ошибкой).

Или всё-таки по нижней планке? Чтобы ошибка была поменьше, правда и сжатие в этом случае будет похуже...

P.S. Вот пример квантования для 6 битов на отсчёт начиная со значения 145 (нижняя планка для Q=49 с усреднённой ошибкой 4% и коэффициентом сжатия K=2.57):

Attachment:
walshexp_117.png

и начиная со значения 125 (верхняя планка для Q=69 с усреднённой ошибкой 5% и коэффициентом сжатия K=2.15):

Attachment:
walshexp_118.png

Как можно видеть в первом случае самым маленькими по амплитуде ненулевыми отсчётами в восстановленной последовательности отсчётов (средний столбик) являются -5 и +5, а во втором -4 и +4 - т.е. когда будем подгонять под требуемое качество нужно будет отбрасывать именно их (т.к. -1 +1 -2 +2 и т.д. уже убиты более грубым квантованием):

Attachment:
6bit-125-145.zip


P.P.S. Вот обе восстановленные картинки рядом увеличенные в 2 раза, чтобы можно было их сравнить визуально (слева Q=49, справа Q=69):

Attachment:
6bit-145vs125.png

Очевидно, что левая картинка чуть более размытая (хоть и с меньшей ошибкой), а вот по шуму даже сложно сказать где больше шумит...


You do not have the required permissions to view the files attached to this post.

_________________
https://mastodon.social/@Shaos :dj:
https://www.youtube.com/@Shaos1973
28 Nov 2023 21:54 WWW
Shaos
Admin
User avatar

Joined: 08 Jan 2003 23:22
Posts: 23398
Location: Silicon Valley
Post Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)
Shaos wrote:
Shaos wrote:
Наверное надо брать по верхней планке - скажем если пользователь заказал Q=60, то в каждой колонке ищем самую верхнюю строчку, где получающееся качество <=60 (в данном примере Q=69) и далее убираем столько -1 и +1 отсчётов, сколько потребуется, чтобы уменьшить процент ненулевых отчётов до нужного числа (60%) и далее считаем коэффициент сжатия для разных вариаций обходов матрицы и способов сжатия - выбираем тот вариант, что меньше (а если размеры получились одинаковыми для разных вариантов, то выбираем вариант с меньшей ошибкой).

Или всё-таки по нижней планке? Чтобы ошибка была поменьше, правда и сжатие в этом случае будет похуже...

Ладно - будет по верхней планке. И поиск можно делать не тупым перебором, а бинарный т.к. коэффициенты сжатия K всегда идут по возрастанию снизу-вверх, а детерминированное качество Q всегда идёт по убыванию снизу-вверх (а вот ошибка нет - она скачет ибо "по нижней планке" ошибка всегда ниже, чем у предыдущей "верхней планки", хотя в пределах одного и того же значения Q ошибка тоже всегда увеличивается снизу-вверх - её придётся подсчитывать на месте уже после выбора точки по которой мы будем работать).

P.S. Смотрю на современные форматы и их алгоритмы во всяких разных статьях в интернете - сейчас стало модным указывать не коэффициент сжатия, а битность на пиксел bpp - например K=2.57 в моём случае стал бы 2.33 bpp, а K=8.96 стал бы 0.66 bpp. Зная K можно легко вычислить битность на пиксел как 6/K (в нашем случае изначально имеется 6 битов на пиксел). Удобство такого представления состоит в том, что по сути не имеет значения сколько бит было изначально в пикселе (это если не вычислять коэффициент сжатия как таковой) - можно считать сколько их стало. И например JPEG2000 на основе вейфлетов даёт показатели 0.32 и 0.25 bpp терпимого качества в случае чёрно-белых изображений, что для меня пока недостижимо (хотя наверное надо попробовать преобразования на больших квадратах типа 512х512 и даже 1024х1024 - там сжатие должно быть сильнее).

_________________
https://mastodon.social/@Shaos :dj:
https://www.youtube.com/@Shaos1973
29 Nov 2023 01:12 WWW
Shaos
Admin
User avatar

Joined: 08 Jan 2003 23:22
Posts: 23398
Location: Silicon Valley
Post Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)
В моём старом коде 1996 года интересно рассчитывается переиндексация спектра Уолша, чтобы он был в порядке увеличения частоты после того, как значения отсчётов получены быстрым преобразованием "бабочками" (FWT = Fast Walsh Transform):
Code:
  for(i=0;i<N;i++) spi[i]=0;
  for(i=0;i<N;i++) spi[0]+=i;
  k=N;j=-N_2;
  while(k!=1)
  { spi[k-1]=j;
    j*=2;
    k/=2;
  }
  FWT(spi);
Получается чтобы вычислить новые индексы, программа выполняет FWT над специально подготовленным массивом - вот его содержимое до FWT:
Code:
[0] 2016
[1] -1024
[2] 0
[3] -512
[4] 0
[5] 0
[6] 0
[7] -256
[8] 0
[9] 0
[10] 0
[11] 0
[12] 0
[13] 0
[14] 0
[15] -128
[16] 0
[17] 0
[18] 0
[19] 0
[20] 0
[21] 0
[22] 0
[23] 0
[24] 0
[25] 0
[26] 0
[27] 0
[28] 0
[29] 0
[30] 0
[31] -64
[32] 0
[33] 0
[34] 0
[35] 0
[36] 0
[37] 0
[38] 0
[39] 0
[40] 0
[41] 0
[42] 0
[43] 0
[44] 0
[45] 0
[46] 0
[47] 0
[48] 0
[49] 0
[50] 0
[51] 0
[52] 0
[53] 0
[54] 0
[55] 0
[56] 0
[57] 0
[58] 0
[59] 0
[60] 0
[61] 0
[62] 0
[63] -32

А вот после FWT (на самом деле тут слегка подправленный FWT - в случае обработки этого массива идёт деление не на sqrt(N) то бишь 8, а просто на N т.е. на 64 - по идее можно поправить изначальный массив так, чтобы делить стандартно на 8):
Code:
[0] 0
[1] 63
[2] 31
[3] 32
[4] 15
[5] 48
[6] 16
[7] 47
[8] 7
[9] 56
[10] 24
[11] 39
[12] 8
[13] 55
[14] 23
[15] 40
[16] 3
[17] 60
[18] 28
[19] 35
[20] 12
[21] 51
[22] 19
[23] 44
[24] 4
[25] 59
[26] 27
[27] 36
[28] 11
[29] 52
[30] 20
[31] 43
[32] 1
[33] 62
[34] 30
[35] 33
[36] 14
[37] 49
[38] 17
[39] 46
[40] 6
[41] 57
[42] 25
[43] 38
[44] 9
[45] 54
[46] 22
[47] 41
[48] 2
[49] 61
[50] 29
[51] 34
[52] 13
[53] 50
[54] 18
[55] 45
[56] 5
[57] 58
[58] 26
[59] 37
[60] 10
[61] 53
[62] 21
[63] 42

Как можно видеть теперь тут индексы для перестановки отсчётов. Совершенно не помню откуда я взял этот алгоритм (помню только, что обратил внимание тогда, что переиндексация в обратную сторону соответствует кодам Грэя, но тут явно не про коды Грэя) - в те времена у нас интернетов ещё небыло (первый интернет на кафедру я провёл лично в конце 1996 года выделенной линией, которую подцепил к линукс-маршрутизатору, который в свою очередь уже раздавал интернет через Ethernet на другие лабораторные компы с Win3.11 и Netscape).

P.S. Чтобы увидеть тут коды Грэя надо переставить строчки в соответствии с новым индексом и представить старый индекс (число в квадратных скобках) в бинарном виде:
Code:
 [0] 0  -> 000000
[32] 1  -> 100000
[48] 2  -> 110000
[16] 3  -> 010000
[24] 4  -> 011000
[56] 5  -> 111000
[40] 6  -> 101000
 [8] 7  -> 001000
[12] 8  -> 001100
[44] 9  -> 101100
[60] 10 -> 111100
[28] 11 -> 011100
[20] 12 -> 010100
[52] 13 -> 110100
[36] 14 -> 100100
 [4] 15 -> 000100
 [6] 16 -> 000110
[38] 17 -> 100110
[54] 18 -> 110110
[22] 19 -> 010110
[30] 20 -> 011110
[62] 21 -> 111110
[46] 22 -> 101110
[14] 23 -> 001110
[10] 24 -> 001010
[42] 25 -> 101010
[58] 26 -> 111010
[26] 27 -> 011010
[18] 28 -> 010010
[50] 29 -> 110010
[34] 30 -> 100010
 [2] 31 -> 000010
 [3] 32 -> 000011
[35] 33 -> 100011
[51] 34 -> 110011
[19] 35 -> 010011
[27] 36 -> 011011
[59] 37 -> 111011
[43] 38 -> 101011
[11] 39 -> 001011
[15] 40 -> 001111
[47] 41 -> 101111
[63] 42 -> 111111
[31] 43 -> 011111
[23] 44 -> 010111
[55] 45 -> 110111
[39] 46 -> 100111
 [7] 47 -> 000111
 [5] 48 -> 000101
[37] 49 -> 100101
[53] 50 -> 110101
[21] 51 -> 010101
[29] 52 -> 011101
[61] 53 -> 111101
[45] 54 -> 101101
[13] 55 -> 001101
 [9] 56 -> 001001
[41] 57 -> 101001
[57] 58 -> 111001
[25] 59 -> 011001
[17] 60 -> 010001
[49] 61 -> 110001
[33] 62 -> 100001
 [1] 63 -> 000001
Как можно видеть в бинарном виде от строчки к строчке меняется всегда ровно один бит (причём оно закручивается в кольцо) т.е. налицо коды Грэя, правда судя по всему реверснутые :egeek:

_________________
https://mastodon.social/@Shaos :dj:
https://www.youtube.com/@Shaos1973
01 Dec 2023 00:06 WWW
Shaos
Admin
User avatar

Joined: 08 Jan 2003 23:22
Posts: 23398
Location: Silicon Valley
Post Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)
Shaos wrote:
В моём старом коде 1996 года интересно рассчитывается переиндексация спектра Уолша, чтобы он был в порядке увеличения частоты после того, как значения отсчётов получены быстрым преобразованием "бабочками" (FWT = Fast Walsh Transform)
...
на самом деле тут слегка подправленный FWT - в случае обработки этого массива идёт деление не на sqrt(N) то бишь 8, а просто на N т.е. на 64 - по идее можно поправить изначальный массив так, чтобы делить стандартно на 8...

И точно - поправил код вот таким образом:
Code:
int i,j,k;
  for(i=0;i<N;i++) spi[i]=0;
  for(i=0;i<N;i++) spi[0]+=i;
  spi[0]/=(int)sqrtN;
  k=N;j=-N_2/(int)sqrtN;
  while(k!=1){spi[k-1]=j;j<<=1;k>>=1;}
  if(store) for(i=0;i<N;i++) store[i]=spi[i];
  FWT(spi);
и теперь внутри FWT всё делиться единообразно для всех случаев на sqrt(N) разве что в случае обработки spi нету перестановки - вот так теперь выглядит входной массив (все значения в 8 раз меньше):
Code:
[0] 252
[1] -128
[2] 0
[3] -64
[4] 0
[5] 0
[6] 0
[7] -32
[8] 0
[9] 0
[10] 0
[11] 0
[12] 0
[13] 0
[14] 0
[15] -16
[16] 0
[17] 0
[18] 0
[19] 0
[20] 0
[21] 0
[22] 0
[23] 0
[24] 0
[25] 0
[26] 0
[27] 0
[28] 0
[29] 0
[30] 0
[31] -8
[32] 0
[33] 0
[34] 0
[35] 0
[36] 0
[37] 0
[38] 0
[39] 0
[40] 0
[41] 0
[42] 0
[43] 0
[44] 0
[45] 0
[46] 0
[47] 0
[48] 0
[49] 0
[50] 0
[51] 0
[52] 0
[53] 0
[54] 0
[55] 0
[56] 0
[57] 0
[58] 0
[59] 0
[60] 0
[61] 0
[62] 0
[63] -4


P.S. Правда это означает, что sqrt(N) должно быть целым числом, значит это работает только для N=4,16,64,256 и т.д. Вот например расчёт для N=16:
Code:
spi before:
[0] 30
[1] -16
[2] 0
[3] -8
[4] 0
[5] 0
[6] 0
[7] -4
[8] 0
[9] 0
[10] 0
[11] 0
[12] 0
[13] 0
[14] 0
[15] -2

spi after:
 [0] 0 
 [1] 15
 [2] 7 
 [3] 8 
 [4] 3 
 [5] 12
 [6] 4 
 [7] 11
 [8] 1 
 [9] 14
[10] 6 
[11] 9 
[12] 2 
[13] 13
[14] 5 
[15] 10

gray codes:
0000  [0] 0 
1000  [8] 1 
1100 [12] 2 
0100  [4] 3 
0110  [6] 4 
1110 [14] 5 
1010 [10] 6 
0010  [2] 7 
0011  [3] 8 
1011 [11] 9 
1111 [15] 10
0111  [7] 11
0101  [5] 12
1101 [13] 13
0101  [9] 14
0001  [1] 15


P.P.S. Пожалуй верну как было - лучше всё таки все 2^n поддерживать, а не через один...

_________________
https://mastodon.social/@Shaos :dj:
https://www.youtube.com/@Shaos1973
01 Dec 2023 23:41 WWW
Shaos
Admin
User avatar

Joined: 08 Jan 2003 23:22
Posts: 23398
Location: Silicon Valley
Post Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)
Shaos wrote:
Вот более полная таблица коэффициентов сжатия K, фактора качества Q и ошибки ERR в зависимости от параметров квантования картинки FEMALER.BWS:
Code:
FEMALER | 10bits/samp | 9bits/sampl | 8bits/sampl | 7bits/sampl | 6bits/sample   | 5bits/sample   |
--------+-------------+-------------+-------------+-------------+----------------+----------------+
   1826 | <<< [0][0] always stored separately in 16 bits (unsigned)           ERR|             ERR|
    388 |*K=1.27 Q=99 | K=1.51 Q=99 | K=1.98 Q=69 | K=3.15 Q=40 | K=4.84 Q=17 9% | K=8.96 Q=8     |
    346 | K=1.27 Q=99 | K=1.48 Q=99 | K=1.94 Q=69 | K=2.72 Q=49 | K=4.52 Q=22 8% | K=7.89 Q=8     |
    283 | K=1.27 Q=99 | K=1.31 Q=99 | K=1.80 Q=69 | K=2.55 Q=49 | K=4.03 Q=28 7% | K=6.78 Q=12    |
    244 | K=1.27 Q=99 |*K=1.28 Q=99 | K=1.60 Q=99 | K=2.13 Q=69 | K=3.37 Q=36 6% | K=5.96 Q=15    |
    199 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.53 Q=99 | K=2.00 Q=69 | K=3.17 Q=36 5% | K=4.90 Q=17 9% |
    157 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.40 Q=99 | K=1.88 Q=69 | K=2.66 Q=49 5% | K=4.48 Q=22 8% |
    148 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.35 Q=99 | K=1.83 Q=69 | K=2.62 Q=49 4% | K=4.10 Q=28 8% |
    145 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.33 Q=99 | K=1.82 Q=69 | K=2.57 Q=49 4% | K=4.10 Q=28 7% |
    125 | K=1.27 Q=99 | K=1.28 Q=99 |*K=1.29 Q=99 | K=1.61 Q=99 | K=2.15 Q=69 5% | K=3.97 Q=28 6% |
    124 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.29 Q=99 | K=1.60 Q=99 | K=2.15 Q=69    | K=3.38 Q=35 7% |
    123 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.29 Q=99 | K=1.60 Q=99 | K=2.15 Q=69    | K=3.37 Q=35 7% |
    119 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.29 Q=99 | K=1.60 Q=99 | K=2.14 Q=69    | K=3.37 Q=35 6% |
    112 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.29 Q=99 | K=1.59 Q=99 | K=2.11 Q=69    | K=3.29 Q=35 6% |
    109 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.29 Q=99 | K=1.58 Q=99 | K=2.11 Q=69    | K=3.28 Q=35 6% |
     97 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.29 Q=99 | K=1.52 Q=99 | K=2.00 Q=69    | K=3.17 Q=35 5% |
     92 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.28 Q=99 | K=1.51 Q=99 | K=1.99 Q=69    | K=2.76 Q=48 6% |
     87 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.28 Q=99 | K=1.49 Q=99 | K=1.96 Q=69    | K=2.75 Q=48 5% |
    ... | ...... Q=99 | ...... Q=99 | ...... Q=99 | ...... Q=99 | ...... Q=69    | ...... Q=48    |
     63 | K=1.27 Q=99 | K=1.28 Q=99 | K=1.28 Q=99 |*K=1.29 Q=99 | K=1.61 Q=99    | K=2.52 Q=48 4% |
    ... | ...... Q=99 | ...... Q=99 | ...... Q=99 | ...... Q=99 | ...... Q=99    | .............. |
     31 | K=1.25 Q=99 | K=1.25 Q=99 | K=1.26 Q=99 | K=1.26 Q=99 |*K=1.27 Q=99 2% | K=1.55 Q=99 4% |

Notes: Diagonal traversal, Huffman only

В каждой колонке звёздочка означает точку с которой (и ниже) кодирование идёт без квантования (т.е. шаг квантования равен 1.0) - при этом качество устанавливается в 99 и отсчёты кодируются как есть без искажений (если не считать отбрасывание дробной части из-за которой ошибка ERR обычно не бывает меньше 2%), а всё что выше звёздочки будет с искажениями (даже если Q=99).

Наверное надо брать по верхней планке - скажем если пользователь заказал Q=60, то в каждой колонке ищем самую верхнюю строчку, где получающееся качество <=60 (в данном примере Q=69) и далее убираем столько -1 и +1 отсчётов, сколько потребуется, чтобы уменьшить процент ненулевых отчётов до нужного числа (60%) и далее считаем коэффициент сжатия для разных вариаций обходов матрицы и способов сжатия - выбираем тот вариант, что меньше (а если размеры получились одинаковыми для разных вариантов, то выбираем вариант с меньшей ошибкой).

По процентам наверное от 99 до 90 делаем без квантования (на уровне звёздочки в каждой колонке), от 89 до следующей перед 99 величине - в данном случае 69 - берём Q=99 по верхней планке, далее по верхней планке Q=69 и т.д. Убирать -1 и +1 чтобы подогнать итоговое качество к заказанному Q по-видимому надо с конца в соответствии с выбранной стратегией обхода матрицы, чтобы выиграть на отбрасывании хвостовых нулей (и если все отсчёты -1 и +1 исчерпались, то надо убирать -2 и +2 и т.д.).

Первый диапазон адаптивного алгоритма готов - пока от 90 до 99 с минимальными искажениями (и отбрасыванием единичек в хвосте для уменьшения Q) на примере всё той же FEMALER.BWS:
Code:
-rw-r--r-- 1 shaos shaos 2344 Dec  3 14:17 F90.WHI
-rw-r--r-- 1 shaos shaos 2349 Dec  3 14:13 F91.WHI
-rw-r--r-- 1 shaos shaos 2356 Dec  3 14:12 F92.WHI
-rw-r--r-- 1 shaos shaos 2365 Dec  3 14:11 F93.WHI
-rw-r--r-- 1 shaos shaos 2370 Dec  3 14:11 F94.WHI
-rw-r--r-- 1 shaos shaos 2374 Dec  3 14:10 F95.WHI
-rw-r--r-- 1 shaos shaos 2377 Dec  3 14:09 F96.WHI
-rw-r--r-- 1 shaos shaos 2377 Dec  3 14:09 F97.WHI
-rw-r--r-- 1 shaos shaos 2377 Dec  3 14:08 F98.WHI
-rw-r--r-- 1 shaos shaos 2383 Dec  3 14:16 F99.WHI
-rw-rw-rw- 1 shaos shaos 3076 Nov 19 13:01 FEMALER.BWS
Вот как оно считало по каждой колонке для каждого Q:
Code:
Q=99 COMPRESS\f99.WHI

$10BIT.WHI S=511 B=10 Q=99 (99) K=1.272 Kmax=1.272 (10) HUF (10) Diag (01)
$09BIT.WHI S=255 B=9 Q=99 (99) K=1.280 Kmax=1.280 (9) HUF (10) Diag (01)
$08BIT.WHI S=127 B=8 Q=99 (99) K=1.286 Kmax=1.286 (8) HUF (10) Diag (01)
$07BIT.WHI S=63 B=7 Q=99 (99) K=1.291 Kmax=1.291 (7) HUF (10) Diag (01) <<<
$06BIT.WHI S=31 B=6 Q=99 (99) K=1.267 Kmax=1.291 (7) HUF (10) Diag (01)

Q=98 COMPRESS\f98.WHI

$10BIT.WHI S=511 B=10 Q=98 (98) K=1.275 Kmax=1.275 (10) HUF (10) Vert (11)
$09BIT.WHI S=255 B=9 Q=98 (98) K=1.283 Kmax=1.283 (9) HUF (10) Vert (11)
$08BIT.WHI S=127 B=8 Q=98 (98) K=1.290 Kmax=1.290 (8) HUF (10) Vert (11)
$07BIT.WHI S=63 B=7 Q=98 (98) K=1.294 Kmax=1.294 (7) HUF (10) Vert (11) <<<
$06BIT.WHI S=31 B=6 Q=98 (98) K=1.270 Kmax=1.294 (7) HUF (10) Vert (11)

Q=97 COMPRESS\f97.WHI

$10BIT.WHI S=511 B=10 Q=97 (97) K=1.275 Kmax=1.275 (10) HUF (10) Vert (11)
$09BIT.WHI S=255 B=9 Q=97 (97) K=1.283 Kmax=1.283 (9) HUF (10) Vert (11)
$08BIT.WHI S=127 B=8 Q=97 (97) K=1.290 Kmax=1.290 (8) HUF (10) Vert (11)
$07BIT.WHI S=63 B=7 Q=97 (97) K=1.294 Kmax=1.294 (7) HUF (10) Vert (11) <<<
$06BIT.WHI S=31 B=6 Q=97 (97) K=1.270 Kmax=1.294 (7) HUF (10) Vert (11)

Q=96 COMPRESS\f96.WHI

$10BIT.WHI S=511 B=10 Q=96 (96) K=1.275 Kmax=1.275 (10) HUF (10) Vert (11)
$09BIT.WHI S=255 B=9 Q=96 (96) K=1.283 Kmax=1.283 (9) HUF (10) Vert (11)
$08BIT.WHI S=127 B=8 Q=96 (96) K=1.290 Kmax=1.290 (8) HUF (10) Vert (11)
$07BIT.WHI S=63 B=7 Q=96 (96) K=1.294 Kmax=1.294 (7) HUF (10) Vert (11) <<<
$06BIT.WHI S=31 B=6 Q=96 (96) K=1.273 Kmax=1.294 (7) RLE+HUF (11) Morton (0000)

Q=95 COMPRESS\f95.WHI

$10BIT.WHI S=511 B=10 Q=95 (95) K=1.275 Kmax=1.275 (10) HUF (10) Vert (11)
$09BIT.WHI S=255 B=9 Q=95 (95) K=1.283 Kmax=1.283 (9) HUF (10) Vert (11)
$08BIT.WHI S=127 B=8 Q=95 (95) K=1.290 Kmax=1.290 (8) HUF (10) Vert (11)
$07BIT.WHI S=63 B=7 Q=95 (95) K=1.296 Kmax=1.296 (7) RLE+HUF (11) Morton (0000) <<<
$06BIT.WHI S=31 B=6 Q=95 (95) K=1.278 Kmax=1.296 (7) RLE+HUF (11) Morton (0000)

Q=94 COMPRESS\f94.WHI

$10BIT.WHI S=511 B=10 Q=94 (94) K=1.275 Kmax=1.275 (10) HUF (10) Vert (11)
$09BIT.WHI S=255 B=9 Q=94 (94) K=1.283 Kmax=1.283 (9) RLE+HUF (11) Morton (0000)
$08BIT.WHI S=127 B=8 Q=94 (94) K=1.292 Kmax=1.292 (8) RLE+HUF (11) B.Shells (0001)
$07BIT.WHI S=63 B=7 Q=94 (94) K=1.298 Kmax=1.298 (7) RLE+HUF (11) B.Shells (0001) <<<
$06BIT.WHI S=31 B=6 Q=94 (94) K=1.280 Kmax=1.298 (7) RLE+HUF (11) Morton (0000)

Q=93 COMPRESS\f93.WHI

$10BIT.WHI S=511 B=10 Q=93 (93) K=1.277 Kmax=1.277 (10) RLE+HUF (11) Diag (01)
$09BIT.WHI S=255 B=9 Q=93 (93) K=1.286 Kmax=1.286 (9) RLE+HUF (11) Diag (01)
$08BIT.WHI S=127 B=8 Q=93 (93) K=1.295 Kmax=1.295 (8) RLE+HUF (11) Diag (01)
$07BIT.WHI S=63 B=7 Q=93 (93) K=1.301 Kmax=1.301 (7) RLE+HUF (11) Diag (01) <<<
$06BIT.WHI S=31 B=6 Q=93 (93) K=1.283 Kmax=1.301 (7) RLE+HUF (11) Diag (01)

Q=92 COMPRESS\f92.WHI

$10BIT.WHI S=511 B=10 Q=92 (92) K=1.283 Kmax=1.283 (10) RLE+HUF (11) Diag (01)
$09BIT.WHI S=255 B=9 Q=92 (92) K=1.292 Kmax=1.292 (9) RLE+HUF (11) Diag (01)
$08BIT.WHI S=127 B=8 Q=92 (92) K=1.300 Kmax=1.300 (8) RLE+HUF (11) Diag (01)
$07BIT.WHI S=63 B=7 Q=92 (92) K=1.306 Kmax=1.306 (7) RLE+HUF (11) B.Diag (0010) <<<
$06BIT.WHI S=31 B=6 Q=92 (92) K=1.288 Kmax=1.306 (7) RLE+HUF (11) Diag (01)

Q=91 COMPRESS\f91.WHI

$10BIT.WHI S=511 B=10 Q=91 (91) K=1.286 Kmax=1.286 (10) RLE+HUF (11) Diag (01)
$09BIT.WHI S=255 B=9 Q=91 (91) K=1.295 Kmax=1.295 (9) RLE+HUF (11) B.Diag (0010)
$08BIT.WHI S=127 B=8 Q=91 (91) K=1.304 Kmax=1.304 (8) RLE+HUF (11) B.Diag (0010)
$07BIT.WHI S=63 B=7 Q=91 (91) K=1.310 Kmax=1.310 (7) RLE+HUF (11) B.Diag (0010) <<<
$06BIT.WHI S=31 B=6 Q=91 (91) K=1.290 Kmax=1.310 (7) RLE+HUF (11) B.Diag (0010)

Q=90 COMPRESS\f90.WHI

$10BIT.WHI S=511 B=10 Q=90 (90) K=1.289 Kmax=1.289 (10) RLE+HUF (11) Morton (0000)
$09BIT.WHI S=255 B=9 Q=90 (90) K=1.297 Kmax=1.297 (9) RLE+HUF (11) Morton (0000)
$08BIT.WHI S=127 B=8 Q=90 (90) K=1.306 Kmax=1.306 (8) RLE+HUF (11) Morton (0000)
$07BIT.WHI S=63 B=7 Q=90 (90) K=1.312 Kmax=1.312 (7) RLE+HUF (11) Morton (0000) <<<
$06BIT.WHI S=31 B=6 Q=90 (90) K=1.292 Kmax=1.312 (7) RLE+HUF (11) Morton (0000)

Программа делает перебор по всем вариациям сжатия (HUF+RLE,HUF,RLE) и по всем шести вариациям обхода спектра - как можно видеть для этой конкретной картинки 7-битное квантование всегда показывало лучший результат, однако вариации алгоритмов сжатия для разных Q отличаются. Ошибка по восстановленной картинке во всех случаях показывается как 2%

_________________
https://mastodon.social/@Shaos :dj:
https://www.youtube.com/@Shaos1973
03 Dec 2023 15:32 WWW
Shaos
Admin
User avatar

Joined: 08 Jan 2003 23:22
Posts: 23398
Location: Silicon Valley
Post Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)
А вот например чёрно-белые картинки с высоким качеством сжимаются плохо:

Attachment:
walshexp_120.png


Quote:
Q=90 COMPRESS\d90.WHI

$11BIT.WHI S=1023 B=11 Q=90 (90) K=1.011 Kmax=1.011 (11) RLE+HUF (11) Morton (0000)
$10BIT.WHI S=511 B=10 Q=90 (90) K=1.019 Kmax=1.019 (10) RLE+HUF (11) Morton (0000)
$09BIT.WHI S=255 B=9 Q=90 (90) K=1.027 Kmax=1.027 (9) RLE+HUF (11) Morton (0000)
$08BIT.WHI S=127 B=8 Q=90 (90) K=1.032 Kmax=1.032 (8) RLE+HUF (11) Morton (0000) <<<
$07BIT.WHI S=63 B=7 Q=90 (90) K=1.017 Kmax=1.032 (8) RLE+HUF (11) Morton (0000)


You do not have the required permissions to view the files attached to this post.

_________________
https://mastodon.social/@Shaos :dj:
https://www.youtube.com/@Shaos1973
03 Dec 2023 15:43 WWW
Shaos
Admin
User avatar

Joined: 08 Jan 2003 23:22
Posts: 23398
Location: Silicon Valley
Post Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)
А вот эта картинка не то, что не сжимается при Q=90, а даже наоборот - расширяется :lol:

Attachment:
walshexp_123.png


Code:
Q=90 COMPRESS\t90.WHI

$10BIT.WHI S=511 B=10 Q=90 (90) K=0.942 Kmax=0.942 (10) HUF (10) Vert (11)
$09BIT.WHI S=255 B=9 Q=90 (90) K=0.947 Kmax=0.947 (9) HUF (10) Vert (11)
$08BIT.WHI S=127 B=8 Q=90 (90) K=0.953 Kmax=0.953 (8) HUF (10) Vert (11) <<<
$07BIT.WHI S=63 B=7 Q=90 (90) K=0.949 Kmax=0.953 (8) HUF (10) B.Shells (0001)


P.S. Презалил результат для этой картинки т.к. тут потребовалось удаление не только -1 и +1, но и -2/+2 для полной корректировки Q (если удалять только -1/+1 то Q корректировалось только до 94), но всё равно - результат получился "расширяющимся"...


You do not have the required permissions to view the files attached to this post.

_________________
https://mastodon.social/@Shaos :dj:
https://www.youtube.com/@Shaos1973
03 Dec 2023 15:55 WWW
Shaos
Admin
User avatar

Joined: 08 Jan 2003 23:22
Posts: 23398
Location: Silicon Valley
Post Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)
С высоким качеством хорошо сжимаются те картинки, где уже спектр подрезан:

Image

Attachment:
walshexp_122.png


Code:
Q=90 COMPRESS\h90.WHI

$11BIT.WHI S=1023 B=11 Q=90 (90) K=3.923 Kmax=3.923 (11) HUF (10) Morton (0000)
$10BIT.WHI S=511 B=10 Q=90 (90) K=3.964 Kmax=3.964 (10) HUF (10) Morton (0000)
$09BIT.WHI S=255 B=9 Q=90 (90) K=4.010 Kmax=4.010 (9) HUF (10) Morton (0000) <<<
$08BIT.WHI S=127 B=8 Q=90 (90) K=3.984 Kmax=4.010 (9) HUF (10) Morton (0000)
$07BIT.WHI S=63 B=7 Q=90 (90) K=3.445 Kmax=4.010 (9) HUF (10) Morton (0000)


P.S. Интересной особенностью этого спектра является то, что ненулевые отсчёты начинаются с -4 и +4 т.к. весь спектр расположен в левом-верхнем квадранте (картинка увеличена в 2 раза и в ней просто нету мелких деталей), поэтому удаление началось именно с них...


You do not have the required permissions to view the files attached to this post.

_________________
https://mastodon.social/@Shaos :dj:
https://www.youtube.com/@Shaos1973
03 Dec 2023 16:34 WWW
Shaos
Admin
User avatar

Joined: 08 Jan 2003 23:22
Posts: 23398
Location: Silicon Valley
Post Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)
Shaos wrote:
Ладно - будет по верхней планке. И поиск можно делать не тупым перебором, а бинарный т.к. коэффициенты сжатия K всегда идут по возрастанию снизу-вверх, а детерминированное качество Q всегда идёт по убыванию снизу-вверх (а вот ошибка нет - она скачет ибо "по нижней планке" ошибка всегда ниже, чем у предыдущей "верхней планки", хотя в пределах одного и того же значения Q ошибка тоже всегда увеличивается снизу-вверх - её придётся подсчитывать на месте уже после выбора точки по которой мы будем работать).

Приступаю к реализации алгоритма "по верхней планке", чтобы покрыть факторы качества ниже 90 - для начала надо пройтись по самой первой строчке таблицы, чтобы узнать верхние Q для каждой колонки. Далее находим нижние значения, от которых надо начинать плясать вверх - они вычисляются элементарно - минимально разумная точка это число, которое можно представить указанным количеством бит без квантования (это я уже умею вычислять - см.выше) либо самое нижнее возможное (у меня количество отчётов "выскочек" ограничено 99, поэтому если там в 99-й позиции уже стоит число, которое невозможно представить без искажений данным количеством бит, то танцуем от этого самого числа вверх). Далее бинарным поиском находим точку "по верхней планке" для Q=99 в каждой колонке и далее скачем вверх (опять же бинарным поиском), чтобы найти следующее Q не равное 99 - в таблице для FEMALER приведённой выше за 99 идёт 69 потом 49 потом 36 потом 28 и т.д. По этим цепочкам чисел выбираем самое ближайшее сверху для задаваемого пользователем значения Q (например если пользователь указал Q=50, то выбираем Q=69) и считаем по уже отработанному алгоритму, отбрасывая лишние единички для подгонки Q и перебирая все способы сжатия и все способы обхода матрицы для каждой из колонок (заранее отбросив все колонки, в которых не попадается выбранное значение Q, чтобы не тратить на них вычислительное время), выбирая лучший вариант в колонке и далее выбираем самое лучшее сжатие среди лучших по колонкам...

_________________
https://mastodon.social/@Shaos :dj:
https://www.youtube.com/@Shaos1973
03 Dec 2023 18:00 WWW
Shaos
Admin
User avatar

Joined: 08 Jan 2003 23:22
Posts: 23398
Location: Silicon Valley
Post Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)
Пока суть да дело прогнал ELAINE.BWS для Q=99 и для Q=90, чисто чтобы сравнить со старыми результатами:



Результаты прогона адаптивного алгоритма:

Code:
Q=99 COMPRESS\e99.WHI

$09BIT.WHI S=255 B=9 Q=99 (99) K=1.171 Kmax=1.171 (9) HUF (10) Diag (01)
$08BIT.WHI S=127 B=8 Q=99 (99) K=1.177 Kmax=1.177 (8) HUF (10) Diag (01)
$07BIT.WHI S=63 B=7 Q=99 (99) K=1.180 Kmax=1.180 (7) HUF (10) Diag (01) <<<
$06BIT.WHI S=31 B=6 Q=99 (99) K=1.168 Kmax=1.180 (7) HUF (10) Diag (01)


Attachment:
walshexp_125.png


Code:
Q=90 COMPRESS\e90.WHI

$09BIT.WHI S=255 B=9 Q=90 (90) K=1.189 Kmax=1.189 (9) HUF (10) Diag (01)
$08BIT.WHI S=127 B=8 Q=90 (90) K=1.195 Kmax=1.195 (8) HUF (10) Diag (01)
$07BIT.WHI S=63 B=7 Q=90 (90) K=1.199 Kmax=1.199 (7) HUF (10) Diag (01) <<<
$06BIT.WHI S=31 B=6 Q=90 (90) K=1.190 Kmax=1.199 (7) HUF (10) B.Shells (0001)


Attachment:
walshexp_124.png


You do not have the required permissions to view the files attached to this post.

_________________
https://mastodon.social/@Shaos :dj:
https://www.youtube.com/@Shaos1973
04 Dec 2023 00:56 WWW
Shaos
Admin
User avatar

Joined: 08 Jan 2003 23:22
Posts: 23398
Location: Silicon Valley
Post Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)
Shaos wrote:
А теперь порешаем интересный вопрос - если мы вводим произвольный размер картинок, то надо быть готовым к тому, что наши квадратики будут обрезаться где не попадя - а именно справа или снизу (т.к. слева и сверху они очевидно будут выровнены по левому и верхнему краям) и надо понять что делать с закрытыми краями, чтобы сжатие занимало как можно меньше места. Очевидные варианты, который приходят в голову:
0. закрашиваем край чёрным
1. закрашиваем край белым
2. копируем туда копию того что остаётся видимым
3. копируем туда зеркальную копию того что остаётся видимым
Соответственно вот такие спектры Уолша у нас получаются для вышеописанных вариантов - для обрезания справа:

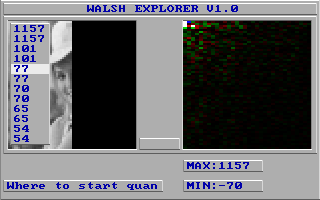
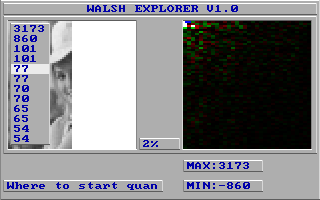
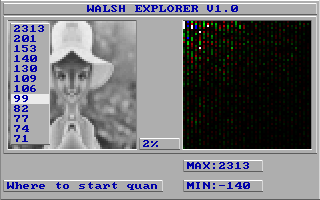
Image

Image

Image

Image

И для обрезания снизу:

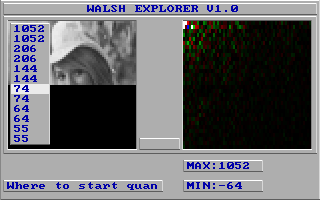
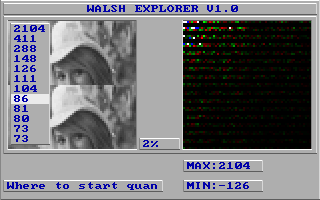
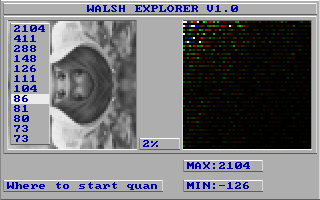
Image

Image

Image

Image

А теперь выясним, какие из этих вариантов лучше всего сжимаются в WHI, если выбирать 6-битное квантование и разные варианты обхода (в названиях файлов они отражаются так - диагональный без дополнительного суффикса, горизонтальный - дополнительный суффикс H, вертикальный - дополнительный суффикс V):
Code:
-rw-r--r-- 1 shaos shaos 1018 Nov 11 22:28 HALF2VV.WHI
-rw-r--r-- 1 shaos shaos 1030 Nov 11 22:30 HALF3VV.WHI
-rw-r--r-- 1 shaos shaos 1064 Nov 11 22:27 HALF2HH.WHI
-rw-r--r-- 1 shaos shaos 1076 Nov 11 22:29 HALF3HH.WHI
-rw-r--r-- 1 shaos shaos 1249 Nov 11 22:28 HALF2VH.WHI
-rw-r--r-- 1 shaos shaos 1271 Nov 11 22:28 HALF2V.WHI
-rw-r--r-- 1 shaos shaos 1297 Nov 11 22:25 HALF1VH.WHI
-rw-r--r-- 1 shaos shaos 1298 Nov 11 23:09 HALF0VH.WHI
-rw-r--r-- 1 shaos shaos 1299 Nov 11 22:27 HALF2HV.WHI
-rw-r--r-- 1 shaos shaos 1324 Nov 11 22:26 HALF2H.WHI
-rw-r--r-- 1 shaos shaos 1367 Nov 11 23:08 HALF0HV.WHI
-rw-r--r-- 1 shaos shaos 1371 Nov 11 22:24 HALF1HV.WHI
-rw-r--r-- 1 shaos shaos 1380 Nov 11 22:30 HALF3VH.WHI
-rw-r--r-- 1 shaos shaos 1410 Nov 11 22:30 HALF3V.WHI
-rw-r--r-- 1 shaos shaos 1424 Nov 11 22:29 HALF3HV.WHI
-rw-r--r-- 1 shaos shaos 1451 Nov 11 22:29 HALF3H.WHI
-rw-r--r-- 1 shaos shaos 1544 Nov 11 22:25 HALF1VV.WHI
-rw-r--r-- 1 shaos shaos 1545 Nov 11 23:09 HALF0VV.WHI
-rw-r--r-- 1 shaos shaos 1547 Nov 11 22:24 HALF1V.WHI
-rw-r--r-- 1 shaos shaos 1548 Nov 11 23:09 HALF0V.WHI
-rw-r--r-- 1 shaos shaos 1589 Nov 11 22:23 HALF1H.WHI
-rw-r--r-- 1 shaos shaos 1589 Nov 11 23:07 HALF0H.WHI
-rw-r--r-- 1 shaos shaos 1592 Nov 11 22:23 HALF1HH.WHI
-rw-r--r-- 1 shaos shaos 1592 Nov 11 23:08 HALF0HH.WHI
-rw-r--r-- 1 shaos shaos 1791 Nov 11 12:32 ELAINE62.WHI <<< целая картинка сжатая методом "Huffman only"
-rw-r--r-- 1 shaos shaos 1827 Nov 11 12:32 ELAINE6H.WHI <<< целая картинка сжатая "Huffman after RLE" с горизонтальным обходом
-rw-r--r-- 1 shaos shaos 1827 Nov 11 12:32 ELAINE6V.WHI <<< целая картинка сжатая "Huffman after RLE" с вертикальным обходом
-rw-r--r-- 1 shaos shaos 1828 Nov 11 22:15 ELAINE6.WHI <<< целая картинка сжатая "Huffman after RLE" с диагональным обходом
-rw-r--r-- 1 shaos shaos 2966 Nov 11 12:32 ELAINE61.WHI <<< целая картинка сжатая "RLE only"
-rw-r--r-- 1 shaos shaos 3093 Nov 11 12:32 ELAINE60.WHI <<< целая картинка сжатая "Raw data"
-rw-r--r-- 1 shaos shaos 3076 Oct 29 00:34 ELAINE.BWS <<< целая картинка - оригинал
Как можно видеть краевая картинка справа (вертикальный отрез) лучше сжимается, если в скрытой части сидит копия видимой части и обход идёт вертикально (HALF2VV.WHI), и краевая картинка снизу (горизонтальный отрез) лучше сжимается, если в скрытой части сидит копия видимой части, но обход идёт уже горизонтально (HALF2HH.WHI). Зеркальные варианты отстают только на 12 байтов (HALF3VV.WHI и HALF3HH.WHI), а варианты с чёрными или белыми половинами судя по всему сжимаются плохо (причём когда обход идёт "перпендикулярно" отрезу, то сжатие несколько лучше).

А теперь всё тоже самое с адаптивным алгоритмом при Q=90

Оригинал:

Code:
Q=90 COMPRESS\elaine90.WHI

$09BIT.WHI S=255 B=9 Q=90 (90) K=1.189 Kmax=1.189 (9) HUF (10) Diag (01)
$08BIT.WHI S=127 B=8 Q=90 (90) K=1.195 Kmax=1.195 (8) HUF (10) Diag (01)
$07BIT.WHI S=63 B=7 Q=90 (90) K=1.199 Kmax=1.199 (7) HUF (10) Diag (01) <<<
$06BIT.WHI S=31 B=6 Q=90 (90) K=1.190 Kmax=1.199 (7) HUF (10) B.Shells (0001)

Chosen $07BIT.WHI for Q=90 S=63 B=7 K=1.199 (5.005 bpp) HUF (10) Diag (01)

Image

Для ВЕРТИКАЛЬНЫХ половинок хуже всего сжимается картинка с чёрной половиной:

Code:
Q=90 COMPRESS\half0v.WHI

$12BIT.WHI S=2047 B=12 Q=90 (90) K=1.402 Kmax=1.402 (12) HUF (10) B.Shells (0001)
$11BIT.WHI S=1023 B=11 Q=90 (90) K=1.524 Kmax=1.524 (11) RLE+HUF (11) Horz (10)
$10BIT.WHI S=511 B=10 Q=90 (90) K=1.532 Kmax=1.532 (10) RLE+HUF (11) Horz (10)
$09BIT.WHI S=255 B=9 Q=90 (90) K=1.539 Kmax=1.539 (9) RLE+HUF (11) Horz (10)
$08BIT.WHI S=127 B=8 Q=90 (90) K=1.547 Kmax=1.547 (8) RLE+HUF (11) Horz (10)
$07BIT.WHI S=63 B=7 Q=90 (90) K=1.547 Kmax=1.547 (7) RLE+HUF (11) Horz (10) <<<
$06BIT.WHI S=31 B=6 Q=90 (90) K=1.538 Kmax=1.547 (7) RLE+HUF (11) Horz (10)

Chosen $07BIT.WHI for Q=90 S=63 B=7 K=1.547 (3.878 bpp) RLE+HUF (11) Horz (10)

Image

Далее картинка с белой половинкой:

Code:
Q=90 COMPRESS\half1v.WHI

$11BIT.WHI S=1023 B=11 Q=90 (90) K=1.527 Kmax=1.527 (11) RLE+HUF (11) Horz (10)
$10BIT.WHI S=511 B=10 Q=90 (90) K=1.532 Kmax=1.532 (10) RLE+HUF (11) Horz (10)
$09BIT.WHI S=255 B=9 Q=90 (90) K=1.540 Kmax=1.540 (9) RLE+HUF (11) Horz (10)
$08BIT.WHI S=127 B=8 Q=90 (90) K=1.547 Kmax=1.547 (8) RLE+HUF (11) Horz (10)
$07BIT.WHI S=63 B=7 Q=90 (90) K=1.549 Kmax=1.549 (7) RLE+HUF (11) Horz (10) <<<
$06BIT.WHI S=31 B=6 Q=90 (90) K=1.541 Kmax=1.549 (7) RLE+HUF (11) Horz (10)

Chosen $07BIT.WHI for Q=90 S=63 B=7 K=1.549 (3.874 bpp) RLE+HUF (11) Horz (10)

Image

И далее картинка с серой половинкой (чисто на пробу):

Code:
Q=90 COMPRESS\half-v.WHI

$09BIT.WHI S=255 B=9 Q=90 (90) K=1.542 Kmax=1.542 (9) RLE+HUF (11) Horz (10)
$08BIT.WHI S=127 B=8 Q=90 (90) K=1.547 Kmax=1.547 (8) RLE+HUF (11) Horz (10)
$07BIT.WHI S=63 B=7 Q=90 (90) K=1.550 Kmax=1.550 (7) RLE+HUF (11) Horz (10) <<<
$06BIT.WHI S=31 B=6 Q=90 (90) K=1.547 Kmax=1.550 (7) RLE+HUF (11) Horz (10)

Chosen $07BIT.WHI for Q=90 S=63 B=7 K=1.550 (3.870 bpp) RLE+HUF (11) Horz (10)

Attachment:
walshexp_126.png


Далее картинка с зеркальной половинкой:

Code:
Q=90 COMPRESS\half3v.WHI

$09BIT.WHI S=255 B=9 Q=90 (90) K=2.073 Kmax=2.073 (9) RLE+HUF (11) Vert (11)
$08BIT.WHI S=127 B=8 Q=90 (90) K=2.093 Kmax=2.093 (8) RLE+HUF (11) Vert (11)
$07BIT.WHI S=63 B=7 Q=90 (90) K=2.110 Kmax=2.110 (7) RLE+HUF (11) Vert (11) <<<
$06BIT.WHI S=31 B=6 Q=90 (90) K=2.062 Kmax=2.110 (7) RLE+HUF (11) Vert (11)

Chosen $07BIT.WHI for Q=90 S=63 B=7 K=2.110 (2.844 bpp) RLE+HUF (11) Vert (11)

Image

И самое лучшее сжатие показывает картинка с двумя одинаковыми половинками:

Code:
Q=90 COMPRESS\half2v.WHI

$09BIT.WHI S=255 B=9 Q=90 (90) K=2.091 Kmax=2.091 (9) RLE+HUF (11) Vert (11)
$08BIT.WHI S=127 B=8 Q=90 (90) K=2.111 Kmax=2.111 (8) RLE+HUF (11) Vert (11) <<<
$07BIT.WHI S=63 B=7 Q=90 (90) K=2.110 Kmax=2.111 (8) RLE+HUF (11) Vert (11)
$06BIT.WHI S=31 B=6 Q=90 (90) K=2.078 Kmax=2.111 (8) RLE+HUF (11) Vert (11)

Chosen $08BIT.WHI for Q=90 S=127 B=8 K=2.111 (2.842 bpp) RLE+HUF (11) Vert (11)

Image

Для ГОРИЗОНТАЛЬНЫХ половинок хуже всего сжимается картинка с белой половиной:

Code:
Q=90 COMPRESS\half1h.WHI

$11BIT.WHI S=1023 B=11 Q=90 (90) K=1.480 Kmax=1.480 (11) RLE+HUF (11) Vert (11)
$10BIT.WHI S=511 B=10 Q=90 (90) K=1.487 Kmax=1.487 (10) RLE+HUF (11) Vert (11)
$09BIT.WHI S=255 B=9 Q=90 (90) K=1.495 Kmax=1.495 (9) RLE+HUF (11) Vert (11)
$08BIT.WHI S=127 B=8 Q=90 (90) K=1.500 Kmax=1.500 (8) RLE+HUF (11) Vert (11)
$07BIT.WHI S=63 B=7 Q=90 (90) K=1.505 Kmax=1.505 (7) RLE+HUF (11) Vert (11) <<<
$06BIT.WHI S=31 B=6 Q=90 (90) K=1.488 Kmax=1.505 (7) RLE+HUF (11) Vert (11)

Chosen $07BIT.WHI for Q=90 S=63 B=7 K=1.505 (3.987 bpp) RLE+HUF (11) Vert (11)

Image

Далее идёт чёрная половина:

Code:
Q=90 COMPRESS\half0h.WHI

$12BIT.WHI S=2047 B=12 Q=90 (90) K=1.378 Kmax=1.378 (12) HUF (10) Vert (11)
$11BIT.WHI S=1023 B=11 Q=90 (90) K=1.485 Kmax=1.485 (11) RLE+HUF (11) Vert (11)
$10BIT.WHI S=511 B=10 Q=90 (90) K=1.493 Kmax=1.493 (10) RLE+HUF (11) Vert (11)
$09BIT.WHI S=255 B=9 Q=90 (90) K=1.500 Kmax=1.500 (9) RLE+HUF (11) Vert (11)
$08BIT.WHI S=127 B=8 Q=90 (90) K=1.506 Kmax=1.506 (8) RLE+HUF (11) Vert (11)
$07BIT.WHI S=63 B=7 Q=90 (90) K=1.510 Kmax=1.510 (7) RLE+HUF (11) Vert (11) <<<
$06BIT.WHI S=31 B=6 Q=90 (90) K=1.490 Kmax=1.510 (7) RLE+HUF (11) Vert (11)

Chosen $07BIT.WHI for Q=90 S=63 B=7 K=1.510 (3.973 bpp) RLE+HUF (11) Vert (11)

Image

Потом зеркальная:

Code:
Q=90 COMPRESS\half3h.WHI

$10BIT.WHI S=511 B=10 Q=90 (90) K=2.024 Kmax=2.024 (10) RLE+HUF (11) Horz (10)
$09BIT.WHI S=255 B=9 Q=90 (90) K=2.045 Kmax=2.045 (9) RLE+HUF (11) Horz (10)
$08BIT.WHI S=127 B=8 Q=90 (90) K=2.064 Kmax=2.064 (8) RLE+HUF (11) Horz (10)
$07BIT.WHI S=63 B=7 Q=90 (90) K=2.080 Kmax=2.080 (7) RLE+HUF (11) Horz (10) <<<
$06BIT.WHI S=31 B=6 Q=90 (90) K=2.024 Kmax=2.080 (7) RLE+HUF (11) Horz (10)

Chosen $07BIT.WHI for Q=90 S=63 B=7 K=2.080 (2.885 bpp) RLE+HUF (11) Horz (10)

Image

И самая сжимаемая картинка с двумя одинаковыми половинками (как и в предыдущем случае):

Code:
Q=90 COMPRESS\half2h.WHI

$10BIT.WHI S=511 B=10 Q=90 (90) K=2.041 Kmax=2.041 (10) RLE+HUF (11) Horz (10)
$09BIT.WHI S=255 B=9 Q=90 (90) K=2.062 Kmax=2.062 (9) RLE+HUF (11) Horz (10)
$08BIT.WHI S=127 B=8 Q=90 (90) K=2.083 Kmax=2.083 (8) RLE+HUF (11) Horz (10) <<<
$07BIT.WHI S=63 B=7 Q=90 (90) K=2.080 Kmax=2.083 (8) RLE+HUF (11) Horz (10)
$06BIT.WHI S=31 B=6 Q=90 (90) K=2.038 Kmax=2.083 (8) RLE+HUF (11) Horz (10)

Chosen $08BIT.WHI for Q=90 S=127 B=8 K=2.083 (2.881 bpp) RLE+HUF (11) Horz (10)

Image

Как можно видеть и для вертикальных, и для горизонтальных половинок лучше всего сжимается вариант, когда обе половинки повторяют друг-друга (как я и писал ранее). Для угловой картинки, когда остаётся только левая-верхняя часть очевидно надо скопировать этот квадрант остальные 3 раза для получения лучшего результата по сжатию.


You do not have the required permissions to view the files attached to this post.

_________________
https://mastodon.social/@Shaos :dj:
https://www.youtube.com/@Shaos1973
05 Dec 2023 00:17 WWW
Shaos
Admin
User avatar

Joined: 08 Jan 2003 23:22
Posts: 23398
Location: Silicon Valley
Post Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)
Далее ещё попробовал с 1/4 и 3/4 вертикальными обрезами

Картинка занимает 1/4 квадрата, остальное серая заливка:

Code:
Q=90 COMPRESS\half-v14.WHI

$07BIT.WHI S=63 B=7 Q=90 (90) K=2.471 Kmax=2.471 (7) RLE+HUF (11) Horz (10) <<<
$06BIT.WHI S=31 B=6 Q=90 (90) K=2.461 Kmax=2.471 (7) RLE+HUF (11) Horz (10)
$05BIT.WHI S=15 B=5 Q=90 (90) K=2.407 Kmax=2.471 (7) RLE+HUF (11) Horz (10)

Chosen $07BIT.WHI for Q=90 S=63 B=7 K=2.471 (2.428 bpp) RLE+HUF (11) Horz (10)

Attachment:
walshexp_128.png

Attachment:
walshexp_134.png


Картинка занимает 1/4 квадрата, остальное занимают 3 её копии - сжимается сильно лучше:

Code:
Q=90 COMPRESS\half2v14.WHI

$09BIT.WHI S=255 B=9 Q=90 (90) K=3.979 Kmax=3.979 (9) RLE+HUF (11) Vert (11) <<<
$08BIT.WHI S=127 B=8 Q=90 (90) K=3.974 Kmax=3.979 (9) RLE+HUF (11) Vert (11)
$07BIT.WHI S=63 B=7 Q=90 (90) K=3.974 Kmax=3.979 (9) RLE+HUF (11) Vert (11)
$06BIT.WHI S=31 B=6 Q=90 (90) K=3.974 Kmax=3.979 (9) RLE+HUF (11) Vert (11)
$05BIT.WHI S=15 B=5 Q=90 (90) K=3.702 Kmax=3.979 (9) RLE+HUF (11) Vert (11)

Chosen $09BIT.WHI for Q=90 S=255 B=9 K=3.979 (1.508 bpp) RLE+HUF (11) Vert (11)

Attachment:
walshexp_130.png

Attachment:
walshexp_133.png


Картинка занимает 3/4 квадрата, остальное серая заливка - сжимается плохо (чуть лучше цельной картинки):

Code:
Q=90 COMPRESS\half-v34.WHI

$09BIT.WHI S=255 B=9 Q=90 (90) K=1.258 Kmax=1.258 (9) RLE+HUF (11) Morton (0000)
$08BIT.WHI S=127 B=8 Q=90 (90) K=1.265 Kmax=1.265 (8) RLE+HUF (11) Morton (0000)
$07BIT.WHI S=63 B=7 Q=90 (90) K=1.272 Kmax=1.272 (7) RLE+HUF (11) Morton (0000) <<<
$06BIT.WHI S=31 B=6 Q=90 (90) K=1.265 Kmax=1.272 (7) RLE+HUF (11) Morton (0000)

Chosen $07BIT.WHI for Q=90 S=63 B=7 K=1.272 (4.718 bpp) RLE+HUF (11) Morton (0000)

Attachment:
walshexp_129.png

Attachment:
walshexp_135.png


Картинка занимает 3/4 квадрата, остальное копия третей четвертины - сжимается ещё хуже (хоть и всё ещё лучше цельной картинки):

Code:
Q=90 COMPRESS\half2v34.WHI

$09BIT.WHI S=255 B=9 Q=90 (90) K=1.242 Kmax=1.242 (9) RLE+HUF (11) Morton (0000)
$08BIT.WHI S=127 B=8 Q=90 (90) K=1.249 Kmax=1.249 (8) RLE+HUF (11) Morton (0000)
$07BIT.WHI S=63 B=7 Q=90 (90) K=1.254 Kmax=1.254 (7) RLE+HUF (11) Morton (0000) <<<
$06BIT.WHI S=31 B=6 Q=90 (90) K=1.239 Kmax=1.254 (7) RLE+HUF (11) Morton (0000)

Chosen $07BIT.WHI for Q=90 S=63 B=7 K=1.254 (4.785 bpp) RLE+HUF (11) Morton (0000)

Attachment:
walshexp_131.png

Attachment:
walshexp_136.png

По сути оно сравнимо по сжимаемости с цельной картинкой - смысла копировании четвертины в данном случае нет - просто заливаем остаток одним тоном (как я уже и писал ранее).

А в случае 1/4 отреза копирование четвертинок даёт лучший результат нежели заливка одним тоном.


You do not have the required permissions to view the files attached to this post.

_________________
https://mastodon.social/@Shaos :dj:
https://www.youtube.com/@Shaos1973
05 Dec 2023 02:19 WWW
Shaos
Admin
User avatar

Joined: 08 Jan 2003 23:22
Posts: 23398
Location: Silicon Valley
Post Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)
После того как закончу адаптивный алгоритм и выкачу версию 1.0.5 надо будет написать полноценный WHI-энкодер для больших картинок (чёрно-белых и цветных) - он будет под ДОС и скорее всего просто будет резать картинку на BWS-файлы размером 64x64 и сжимать их запуская WALSHEXP.EXE много-много раз через автоматизацию (которую я добавил ещё в версии 1.0.4) по сгенерированному программно скрипту - так для меня будет быстрее всего.

А вот WHI-декодер больших картинок уже можно будет начать писать под линух - для начала конвертер из командной строки в PNG и/или TIFF, а далее уже можно и прототип nedopixels городить :lol:

Или лучше сначала сделать плугин для GIMP?

Или аддон для Firefox?...

_________________
https://mastodon.social/@Shaos :dj:
https://www.youtube.com/@Shaos1973
05 Dec 2023 03:03 WWW
 Page 4 of 5
  [ 65 posts ]  Go to page Previous  1, 2, 3, 4, 5  Next

Board index » NEDOPC IN RUSSIAN » Проект nedoPC

All times are UTC - 8 hours [ DST ]

Who is online

Users browsing this forum: No registered users and 2 guests

You cannot post new topics in this forum
You cannot reply to topics in this forum
You cannot edit your posts in this forum
You cannot delete your posts in this forum
You cannot post attachments in this forum

Jump to:  
Powered by phpBB® Forum Software © phpBB Group
Designed by ST Software.