Lavr wrote:схема полного однотритного сумматора из разработанных мной блоков выглядит
следующим образом:
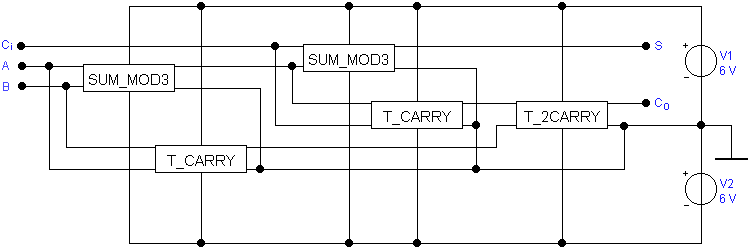
Я на момент создания не сделал никакой проверки полного троичного сумматора, заложившись
на правильную работу отдельных его функциональных блоков.
Это не от лени, а потому как
EWB "захлебывается" считать такую большую аналоговую схему
да еще и вкупе со счетчиком.
Но главное во всей этой затее было то, что я просчитал все необходимые элементы троичной логики аналоговыми методами, то есть, в отличие от чисто цифровых расчетов, здесь учитывались все переходные процессы, проскакивание перехода
[+1] -> [-1] через логический уровень
[0] (
да, это приводит к некоторым "артефактам", но с точки зрения цифровой схемотехники они не смертельны), и пришел я к основному выводу, что аналоговые модели соответствуют алгебре троичной логики, а поэтому можно было осуществить качественный скачок, перейдя к чисто цифровым моделям для повышения скорости расчета.
В качестве платформы я выбрал
Proteus, поскольку разработчики заложили в его движок
логическое состояние "конфликта", очень хорошо соответствующее нашему понятию "неопределённости" в троичке: это состояние
Proteus трактует как уровень 2.5 В, что вполне подходит для моделирования устройств на троичной логике.

Ну и поскольку
dll-библиотеки Proteus на C++ мы писать научились, я занялся тем, что уже испытанные аналоговые модели элементов троичной логики перевёл в цифровой вид:

При этом старался сравнивать идентичность поведения цифровых моделей с аналоговыми:

Интересно, что в результате этих изысканий фактически пришлось разработать семейство троичных логических элементов, поскольку
Proteus при компиляции предлагает упаковать логику в подхоящий корпус, и я попытался сделать это в полной аналогии с существующими сериями
74... 74LS... 74HC..., где одинаковым логическим элементам присваивают одинаковые номера.
Хотя пришлось "пристроить" и элементы, которых в двоичных сериях просто нет.
Я не выкладывал эти модели в форум, поскольку считаю, что они имеют версию "альфа", то есть, их ошибки и аномалии на начальном этапе должен тщательно вычистить сам разработчик, после чего он (разработчик) приходит к решению, что модели дозрели стать версией "бета", и можно предоставить их на тестирование "бета"-тестерам.
Ну а тестировать логические элементы лучше всего что-то конструируя из них, и я решил начать с троичного сумматора, поскольку в
EWB он был самой тормозной конструкцией.
Конструировал сумматор я по полной аналогии с тем, что уже было сделано ранее в этой ветке форума.
Сначала это была вот такая конструкция из "элементарных кирпичиков" троичной логики:

Потом, после тщательной проверки, я "свернул" её в более компактные модули:

И в итоге получилась вот такая модель полного однотритного сумматора, который я и использовал в АЛУ моего
весьма удачного проекта троичного компьютера.

Если спросить: а в чем смысл такой последовательности? А смысл в том, что для приемлемой скорости моделирования сама модель,
как я вот здесь уже писал, должна быть простой, но адекватной.
То есть, в итоговую "коробочку" полного однотритного сумматора вошли только его "формулы", а не формулы всех элементарных элементов, но сравнение модели сумматора с его же моделью из "элементарных кирпичиков" показало его полную адекватность.
Вот только работает его модель шустрее, чем 10...20 "элементарных кирпичиков".
Ну и так вышло, что
я немного отвлёкся в сторону и написал под Proteus модели популярных здесь у нас мультиплексоров на основе аналоговых ключей DG403.
Чтобы у заинтересованных посетителей форума была возможность не только почитать здесь про троичность, но и хоть как-то приобщиться к процессу...

Благо
Proteus супер-новый не нужен, я всё это делаю под версией
6.7 Pro, которая "вертится" у меня на любимом моём фактически ныне музейном ноутбуке
ThinkPad 600е P-II 366 MHz под
Windows 98.

Ну если у меня "вертится", то у всех должно летать со свистом! (Я проверял на работе на современном десктопе под
Win 10).
Ну и поскольку на моих моделях "муксов" никто и ничего сконструировать не отважился, я решил проверить их адекватность сам как раз вот на примере полного однотритного сумматора.
Получилось в итоге вот что:

Где в каждой коробочке под названием "MUX" для компактности находится вот это:

Я немного перекомпоновал проверенную здесь уже трижды таблицу истинности полного однотритного сумматора, чтобы результаты стало проверять удобнее и логичнее...

Но Proteus-модель полного однотритного сумматора ей полностью соответствует!

На этом можно было бы и закончить... но поскольку у нас у всех на дворе пандемия, и у многих в доме самоизоляция, я подумал, что неплохо бы развлечься и сделать "подляну мерзкую" всем, кто тут скулит уныло и норовит обвинить меня в излишней склонности к счетоводству...

Поэтому я решил собрать эту конструкцию на макетке, благо
DG403 у меня были и время есть.
То, что добротно посчитано, собирается обычно за один вечер или где-то с 12 до 4 утра по моим привычкам.
Так что запаситесь попкорном, продолжение сейчас будет...
















