Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)

Публичный форум для http://www.nedopc.org/nedopc

Moderator: Shaos

User avatar
Shaos
Admin
Posts: 23763
Joined: 08 Jan 2003 23:22
Location: Silicon Valley

Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)

Post by Shaos »

UPDATE: Самые последние исходники под MIT-лицензией всегда можно найти тут: https://gitlab.com/shaos/graphin
Приаттачиваю архив с исходниками и досовским EXE-шником Walsh Explorer v1.0.5 от 7 декабря 2023 года прямо сюда:
GRAPHIN.ZIP
[/b]-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

На основе моей дипломной работы 1996 года хочу зарелизить опенсорсную программу "Walsh Explorer" (для начала под DOS), которая поможет создать простой алгоритм сжатия изображений с потерями, способный заменить JPEG на ретрокомпах (т.к. JPEG для них тяжеловат). В этом простом алгоритме вместо DCT будет использоваться преобразование Уолша (Walsh-Hadamard Transform) и далее кодирование по Хаффману (Huffman coding). Предварительные эксперименты тут показали, что пободаться с JPEG нам вполне по силам :idea:

Отпочковано отсюда: viewtopic.php?f=46&t=22127&start=30
Shaos wrote:А так-то я обработкой изображений очень давно занимаюсь - вот скрины из моей дипломной работы 1996 года:

Image

там например можно было поиграться со спектром преобразования Уолша:

Image

и даже получить обратно картинку из урезанного спектра:

Image

программа работала с BWS форматом изрбражений (это мой собственный формат представления картинок в градациях серого без потерь с 6 битами на точку):

Image

интерфейс пользователя был самописный ( я его создал в 1995 году и назвал GRAPHIN : ) т.к. всё работало на голом досе в 320x200:

Image

как можно видеть я там реализовал несколько простых фильтров и ещё в этой программе можно было поиграться с экспериментальными алгоритмами фрактального сжатия и самодельной "аппроксимации сферами" (тоже моё изобретение):

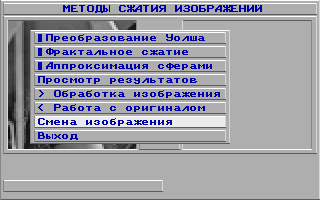
Image
Вот полное меню для преобразования Уолша:
demo_006.png
Откуда можно зайти в "Обработку спектра":
demo_007.png
И выбрать "Просмотр строк спектра" где двигаясь вверх-вниз можно поглядеть глазами как оно выглядит "сбоку":
demo_008.png
А вот подменю "Квантование спектра":
demo_009.png
Где можно огрубить отсчёты скажем до 7 бит и получить восстановленное изображение:
demo_010.png
Надо все эти возможности повторить в нашем новом графическом редакторе :mrgreen:

P.S. IC1 это был мой экспериментальный формат сжатия картинок на основе преобразования Уолша - там тоже надо было квантовать отсчёты, но я там в те времена накосячил с памятью и оно падало при попытке прочитать сохранённый файл (починил 30 октября 2023). Ещё в этой программе был формат IC2 (фрактальное сжатие - для него даже отдельный просмотрщик был) и формат IC3 (моё самодельное сжатие сферами) - ни то, ни другое в настоящее время интереса не вызывает. Ещё судя по архиву наработок я пытался Фурье осилить, но видать не осилил :roll:

P.P.S. Между прочим не всегда спектр Уолша выглядит как непонятное облако - вот например интересный вариант:
demo_011.png
Это я пытался повторить вот этот эксперимент со спектром Фурье (картинка из твиттера):
Fourier.png
You do not have the required permissions to view the files attached to this post.
Я тут за главного - если что шлите мыло на me собака shaos точка net
Top
User avatar
Shaos
Admin
Posts: 23763
Joined: 08 Jan 2003 23:22
Location: Silicon Valley

Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)

Post by Shaos »

Мой формат (слева) до Хаффмана по качеству превосходит пережатый JPEG, но по размерам не догоняет - нужен Хаффман:

Image

Плюс существующий формат надо несколько обработать напильником:
Shaos wrote:В своей дипломной работе 1996 года (см. тут) я сжимал изображения с использованием двумерного спектра Уолша (64x64 для картинок в градациях серого 64х64 где каждый пиксел принимал значения от 0 до 63):



сохраняя его в файл побитно следующим образом:
  • Пользователь спрашивался сколько бит на отсчёт надо использовать для кодирования - выбиралось значение от 4 до 12 (это с учётом бита знака);
  • Отсчёты [0][0], [0][1] и [1][0] сохранялись отдельно в заголовке как целые 14-битные числа (т.к. они обычно сильно больше остальных отсчётов);
  • Параметры квантования (количество битов и шаг с точностью до десятых долей) также сохранялись в заголовке;
  • Остальные отсчёты квантовались от нуля до абсолютного максимума в пределах этого спектра (без учёта вышеупомянутых трёх отсчётов) и сохранялись в указанном количестве битов (с битом знака идущим первым), однако код 100...00 (минус ноль) использовался как маркер последовательности квантованных нулей - если такой маркер встречался в последовательности, то за ним шло 6-битное количество нулей которые надо вставить при вычитке этой строки спектра (таким способом я кодировал 3 и больше нулей идущих подряд).
а именно:
  • Сделать возможным сохранять несколько произвольных отсчётов-выскочек в количестве от 1 до скажем 8 с указанием координат вместо теперешних трёх захардкоденных;
  • Сохранять параметры квантования с большей точностью, а не как сейчас с точностью до десятых долей;
  • Разрешить несколько способов обхода спектра - по горизонтали, по вертикали и по диагонали;
  • Отбрасывать нулевые отсчёты в хвосте спектра для уменьшения размеров получающегося файла;
  • Добавить адаптивное сжатие, когда параметры будут выбираться автоматически исходя из указанного показателя качества (от 0 до 100 по аналогии с JPEG) и если Хаффман не помогает уменьшить блок (если таблица получилась слишком большая), то оставлять RLE (как сейчас).
Ну и в дальнейшем хотелось бы перейти от картинок 64х64 к картинкам произвольного размера (скажем до 2048x2048 кодируя всё те же блоки 64х64 быстрым преобразованием Уолша) - расширение такого файла будет скажем .whi (Walsh+Huffman Image), а если оно таки полетит как надо (под DOS и на ретрокомпах типа Спринтера), то вот тогда уже можно перейти к разработке формата TONIC...
Я тут за главного - если что шлите мыло на me собака shaos точка net
Top
User avatar
shiny
Maniac
Posts: 324
Joined: 14 Oct 2023 06:59

Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)

Post by shiny »

А маркер комментариев поддерживается, или он чуждый классу пользователей?
Top
User avatar
Shaos
Admin
Posts: 23763
Joined: 08 Jan 2003 23:22
Location: Silicon Valley

Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)

Post by Shaos »

shiny wrote:А маркер комментариев поддерживается, или он чуждый классу пользователей?
Кто такой есть маркер комментариев?

В смысле как в JPEG? https://habr.com/en/articles/102521/

Не - комментарии лишние :mrgreen:
Я тут за главного - если что шлите мыло на me собака shaos точка net
Top
imsushka
Maniac
Posts: 212
Joined: 01 Jan 2022 04:34
Location: USSR, Tashkent

Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)

Post by imsushka »

Shaos wrote:Кто такой есть маркер комментариев?

В смысле как в JPEG? https://habr.com/en/articles/102521/

Не - комментарии лишние :mrgreen:
а как же хеш, говорящий что это не генерированная ИИ картинка ?
Top
User avatar
Shaos
Admin
Posts: 23763
Joined: 08 Jan 2003 23:22
Location: Silicon Valley

Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)

Post by Shaos »

imsushka wrote:а как же хеш, говорящий что это не генерированная ИИ картинка ?
ну про то чем сгенерирована сжимаемая картинка кодировщик точно знать не знает
Я тут за главного - если что шлите мыло на me собака shaos точка net
Top
User avatar
shiny
Maniac
Posts: 324
Joined: 14 Oct 2023 06:59

Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)

Post by shiny »

Shaos wrote:Кто такой есть маркер комментариев?

В смысле как в JPEG? https://habr.com/en/articles/102521/

Не - комментарии лишние :mrgreen:
да, это он - COM (FF FE)
вообще, если взглянуть на состав картинки, то обнаружится немало мусора 8)
Top
User avatar
Shaos
Admin
Posts: 23763
Joined: 08 Jan 2003 23:22
Location: Silicon Valley

Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)

Post by Shaos »

Американизированный вариант программы практически готов :mrgreen:
walshexp.gif
Сама программа будет под GPL или MIT (позже решил, что MIT), а используемые библиотечные классы я скорее всего выкачу как PUBLIC DOMAIN:
  • BWS.CPP - Black-and-White Screen format (картинки в градациях серого размером до 65535x65535 пикселов с уровнями яркости от 0 до 63);
  • BITIO.CPP - BIT Input/Output (побитное чтение и сохранение файлов);
  • UNIHUFF.CPP - Huffman coding (чтение и сохранение файлов с кодированием по Хаффману);
  • GRAPHIN.CPP - GRAPHical INterface for DOS (пользовательский интерфейс для досовских программ с кнопками и менюшками) - позже решил графина таки оставить копирайтнутым под MIT-лицензией
( они все созданы мной в 1995-1996 годах, даже Хаффман, которого я тогда так никуда и не прикрутил ибо застрял на отладке : )

P.S. Кстати GRAPHIN умеет поддерживать разрешения до 1024x768 :o

Code: Select all

#define SVGA256_320x200 0
#define SVGA256_640x400 1
#define SVGA256_640x480 2
#define SVGA256_800x600 3
#define SVGA256_1024x768 4
Пример под спойлером:

 1024x768
graftst1_000.png

Правда поддерживает он все эти SVGA режимы через бинарную либу SVGA256.OBJ, которую я где-то оттопырил в 1995 году:

Code: Select all

SVGA 256 Colour BGI Device Driver (SVGA256) 2.31 - Dec 06, 1991 
Copyright (c) 1991 Jordan Hargraphix
О - есть новая версия опенсорц (MIT 2020), которая ещё и разрешение 1280х1024 поддерживает :esurprised:
https://github.com/jharg93/SvgaBGI/blob/main/SVGA256.H
REGISTRATION: I have decided to release these drivers free of charge, although donations would be greatly appreciated and certainly expedite the release of future versions. :-> The drivers have not been crippled in any way, though beta releases of new drivers may have some functions yet unimplemented.

Registration fees: ( Price includes both BGIv2.0 and BGIv3.0 drivers )
...
SuperVGA BGI 256 $30
...
Надо что ли перевести денег человеку, раз уж я аж на протяжении 28 лет его труды использую :roll:

P.P.S. У нас на форуме GRAPHIN упоминался ещё в 2012 году (11 лет назад) в контексте самодельных пользовательских интерфейсов:
viewtopic.php?p=97574#p97574
Решил его выкатить под MIT-лицензией и потом потихоньку развивать до полноценного GUI :roll:
Например очень сильно не мешало бы прикрутить к нему мышь - наработки по мыше для борланда у меня были...
You do not have the required permissions to view the files attached to this post.
Я тут за главного - если что шлите мыло на me собака shaos точка net
Top
User avatar
Shaos
Admin
Posts: 23763
Joined: 08 Jan 2003 23:22
Location: Silicon Valley

Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)

Post by Shaos »

Читаю тут про то как люди меряют качество восстановленной картинки по сравнению с оригиналом:

https://en.wikipedia.org/wiki/Peak_signal-to-noise_ratio

Вот как я в 1996 году считал ошибку, называя её СКО (средне-квадратичное отклонение), коим оно НЕ является:

Code: Select all

double operator|(BWS &b1,BWS &b2)
{ double e,d,d2,n,s;
  e=0.0;s=0.0;
  int i,j,c,r;
  c=b1.GetCol();
  r=b1.GetRow();
  if((c==b2.GetCol())&&(r==b2.GetRow()))
  {   for(i=0;i<c;i++){
      for(j=0;j<r;j++){
          d2=b1.GetPixelScr(i,j);
          d=d2-b2.GetPixelScr(i,j);
          e+=d*d;
          s+=d2*d2;
      }}
      e=sqrt(e/s);
  }
  else e=99999;
  return e;
}
и показывая её в процентах (т.е. умножал на 100). Это не совсем MSE (Median-Squared Error) т.к. в этом случае мне было бы достаточно сложить возведённые в квадрат разницы и разделить на кол-во пикселов, а я делю на сумму яркостей пикселов первой картинки (т.е. уже своего рода нормализованная ошибка) да ещё и беру квадратный корень - получается у совсем различных изображений ошибка будет приближаться к 100%, а у одинаковых - к нулю (наверное по научному это NRMSE - Normalized Root Mean Square Error), однако я заметил что в визуально похожих картинках, где много чёрных пикселов у меня насчитывется большая ошибка - надо разобраться:
walshexp_001.png
P.S. Да - это NRMSE, которое ещё называют коэффициентом вариации или относительным стандартным отклонением если оно измеряется в процентах (как у меня):

https://en.wikipedia.org/wiki/Coefficient_of_variation
Недостатки

1. Когда среднее значение близко к нулю, коэффициент вариации приближается к бесконечности и поэтому чувствителен к небольшим изменениям среднего...
P.P.S. Так то оно вполне терпимо меряет - вот примеры похожих и непохожих изображений:
You do not have the required permissions to view the files attached to this post.
Я тут за главного - если что шлите мыло на me собака shaos точка net
Top
User avatar
Shaos
Admin
Posts: 23763
Joined: 08 Jan 2003 23:22
Location: Silicon Valley

Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)

Post by Shaos »

Shaos wrote:Между прочим не всегда спектр Уолша выглядит как непонятное облако - вот например интересный вариант:

Image
Поправил раскрашивание спектра при выводе - теперь зелёные цвета это положительные отсчёты, а красные - отрицательные. И убрал умножение на 2 из-за которого при отрисовке выпячивались маленькие отсчёты, а большие уходили в разноцветную мешанину, т.к. убегали за пределы своих цветовых диапазонов (сейчас зашкал больше +63 даёт белый, а меньше -64 даёт ярко синий):
You do not have the required permissions to view the files attached to this post.
Я тут за главного - если что шлите мыло на me собака shaos точка net
Top
User avatar
Shaos
Admin
Posts: 23763
Joined: 08 Jan 2003 23:22
Location: Silicon Valley

Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)

Post by Shaos »

Предварительные результаты с Хаффманом - мы его сделали я щитаю (JPEG в смысле) :lol:
WHIvsJPEG.jpg
Можно ещё над более оптимальным представлением таблицы Хаффмана поработать, но результат уже вполне себе...
You do not have the required permissions to view the files attached to this post.
Я тут за главного - если что шлите мыло на me собака shaos точка net
Top
User avatar
Shaos
Admin
Posts: 23763
Joined: 08 Jan 2003 23:22
Location: Silicon Valley

Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)

Post by Shaos »

А вот так будет выглядеть слегка пережатый Уолш в цвете (слева - оригинал, справа - результат восстановления):
TiffanyRGB.png
Это я в GIMP совместил как RGB три картинки в градациях серого, поджатые Уолшем-Хаффманом почти в 3 раза!

И я не планирую прореживать цвета, как это делает JPEG и другие форматы сжатия цветных изображений...
You do not have the required permissions to view the files attached to this post.
Я тут за главного - если что шлите мыло на me собака shaos точка net
Top
User avatar
Shaos
Admin
Posts: 23763
Joined: 08 Jan 2003 23:22
Location: Silicon Valley

Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)

Post by Shaos »

Shaos wrote:
  • Сделать возможным сохранять несколько произвольных отсчётов-выскочек в количестве от 1 до скажем 8 с указанием координат вместо теперешних трёх захардкоденных;
  • Сохранять параметры квантования с большей точностью, а не как сейчас с точностью до десятых долей;
  • Разрешить несколько способов обхода спектра - по горизонтали, по вертикали и по диагонали;
  • Отбрасывать нулевые отсчёты в хвосте спектра для уменьшения размеров получающегося файла;
  • Добавить адаптивное сжатие, когда параметры будут выбираться автоматически исходя из указанного показателя качества (от 0 до 100 по аналогии с JPEG) и если Хаффман не помогает уменьшить блок (если таблица получилась слишком большая), то оставлять RLE (как сейчас).
Реализовал всё, кроме последнего пункта - адаптивный алгоритм будет позже.

По поводу обхода - пока получается, что диагональный обход убирает больше всего хвостовых нулей подряд, чем горизонтальный или вертикальный способы обхода - когда буду делать адаптивный алгоритм надо будет ещё проверять если сжатие может быть лучше при каких-то других обходах, но пока диагональный даёт лучший результат...
Я тут за главного - если что шлите мыло на me собака shaos точка net
Top
User avatar
Shaos
Admin
Posts: 23763
Joined: 08 Jan 2003 23:22
Location: Silicon Valley

Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)

Post by Shaos »

Переделываю сохранение таблицы Хаффмана в соответствии с новой информацией

По ходу можно прикинуть разницу в размерах таблицы в случае 3 разных вариантов сохранения, скажем можно взять таблицу из ELAINE сжатой до 2 бит на сэмпл (ELAINE02.WHI):

Code: Select all

72	088:10
72	086:11
18	175:001
17	176:0111
11	177:0100
7	180:01011
6	178:01010
4	185:011001
3	187:000111
3	183:011000
2	179:000000
2	214:0110100
2	190:0110101
2	182:0110110
2	181:0110111
1	246:0000010
1	223:0000011
1	221:0000100
1	209:0000101
1	204:0000110
1	197:0000111
1	191:0001000
1	189:0001001
1	188:0001010
1	186:0001011
1	184:0001100
1	087:0001101
(таблица Хаффмана в WHI смешивает в месте квантованные отсчёты и метки последовательностей нулей разной длины, представляя их как разные литералы)

Если оставить как есть сейчас, то она будет занимать (3+8)*27+2*2+1*3+2*4+2*5+4*6+7*16=458 бит (58 байт)

Если сделать как SHAFF2 (когда размер символа указывается не для каждого символа, а для целого блока, которых тут 6), но в побитовом сохранении, то уже 8*27+(2+3)*6+2*2+1*3+2*4+2*5+4*6+7*16=407 бит (51 байт)

Если же таблицу упорядочить в соответствии с кодами, то можно сохранить её в виде дерева:

Code: Select all

72 086:11
72 088:10
17 176:0111
2  181:0110111
2  182:0110110
2  190:0110101
2  214:0110100
4  185:011001
3  183:011000
7  180:01011
6  178:01010
11 177:0100
18 175:001
3  187:000111
1  087:0001101
1  184:0001100
1  186:0001011
1  188:0001010
1  189:0001001
1  191:0001000
1  197:0000111
1  204:0000110
1  209:0000101
1  221:0000100
1  223:0000011
1  246:0000010
2  179:000000
получив 269 бит (34 байта) - под спойлером раскладка в дерево:

 дерево

Code: Select all

>>>halfhuf 0..27 (5)- split
offset 5 - 0..1,2..26
	there is 0 branch - process
>>>halfhuf 2..26 (6)- split
offset 6 - 2..11,12..26
	there is 0 branch - process
>>>halfhuf 12..26 (7)- split
offset 7 - 12..12,13..26
	there is 0 branch - process
>>>halfhuf 13..26 (8)- split
offset 8 - 13..19,20..26
	there is 0 branch - process
>>>halfhuf 20..26 (9)- split
offset 9 - 20..23,24..26
	there is 0 branch - process
>>>halfhuf 24..26 (10)- split
offset 10 - 24..25,26..26
	single 0 branch - literal 26 0xB3 ( ) 000000|0
	there is 1 branch - process
>>>halfhuf 24..25 (11)- split
offset 11 - 24..24,25..25
	single 0 branch - literal 25 0xF6 ( ) 0000010|0
	single 1 branch - literal 24 0xDF ( ) 0000011|1
<<<halfhuf 19
<<<halfhuf 29
	there is 1 branch - process
>>>halfhuf 20..23 (10)- split
offset 10 - 20..21,22..23
	there is 0 branch - process
>>>halfhuf 22..23 (11)- split
offset 11 - 22..22,23..23
	single 0 branch - literal 23 0xDD ( ) 0000100|0
	single 1 branch - literal 22 0xD1 ( ) 0000101|1
<<<halfhuf 19
	there is 1 branch - process
>>>halfhuf 20..21 (11)- split
offset 11 - 20..20,21..21
	single 0 branch - literal 21 0xCC ( ) 0000110|0
	single 1 branch - literal 20 0xC5 ( ) 0000111|1
<<<halfhuf 19
<<<halfhuf 39
<<<halfhuf 69
	there is 1 branch - process
>>>halfhuf 13..19 (9)- split
offset 9 - 13..15,16..19
	there is 0 branch - process
>>>halfhuf 16..19 (10)- split
offset 10 - 16..17,18..19
	there is 0 branch - process
>>>halfhuf 18..19 (11)- split
offset 11 - 18..18,19..19
	single 0 branch - literal 19 0xBF ( ) 0001000|0
	single 1 branch - literal 18 0xBD ( ) 0001001|1
<<<halfhuf 19
	there is 1 branch - process
>>>halfhuf 16..17 (11)- split
offset 11 - 16..16,17..17
	single 0 branch - literal 17 0xBC ( ) 0001010|0
	single 1 branch - literal 16 0xBA ( ) 0001011|1
<<<halfhuf 19
<<<halfhuf 39
	there is 1 branch - process
>>>halfhuf 13..15 (10)- split
offset 10 - 13..13,14..15
	there is 0 branch - process
>>>halfhuf 14..15 (11)- split
offset 11 - 14..14,15..15
	single 0 branch - literal 15 0xB8 ( ) 0001100|0
	single 1 branch - literal 14 0x57 (W) 0001101|1
<<<halfhuf 19
	single 1 branch - literal 13 0xBB ( ) 000111|1
<<<halfhuf 29
<<<halfhuf 69
<<<halfhuf 139
	single 1 branch - literal 12 0xAF ( ) 001|1
<<<halfhuf 149
	there is 1 branch - process
>>>halfhuf 2..11 (7)- split
offset 7 - 2..8,9..11
	there is 0 branch - process
>>>halfhuf 9..11 (8)- split
offset 8 - 9..10,11..11
	single 0 branch - literal 11 0xB1 ( ) 0100|0
	there is 1 branch - process
>>>halfhuf 9..10 (9)- split
offset 9 - 9..9,10..10
	single 0 branch - literal 10 0xB2 ( ) 01010|0
	single 1 branch - literal 9 0xB4 ( ) 01011|1
<<<halfhuf 19
<<<halfhuf 29
	there is 1 branch - process
>>>halfhuf 2..8 (8)- split
offset 8 - 2..2,3..8
	there is 0 branch - process
>>>halfhuf 3..8 (9)- split
offset 9 - 3..6,7..8
	there is 0 branch - process
>>>halfhuf 7..8 (10)- split
offset 10 - 7..7,8..8
	single 0 branch - literal 8 0xB7 ( ) 011000|0
	single 1 branch - literal 7 0xB9 ( ) 011001|1
<<<halfhuf 19
	there is 1 branch - process
>>>halfhuf 3..6 (10)- split
offset 10 - 3..4,5..6
	there is 0 branch - process
>>>halfhuf 5..6 (11)- split
offset 11 - 5..5,6..6
	single 0 branch - literal 6 0xD6 ( ) 0110100|0
	single 1 branch - literal 5 0xBE ( ) 0110101|1
<<<halfhuf 19
	there is 1 branch - process
>>>halfhuf 3..4 (11)- split
offset 11 - 3..3,4..4
	single 0 branch - literal 4 0xB6 ( ) 0110110|0
	single 1 branch - literal 3 0xB5 ( ) 0110111|1
<<<halfhuf 19
<<<halfhuf 39
<<<halfhuf 59
	single 1 branch - literal 2 0xB0 ( ) 0111|1
<<<halfhuf 69
<<<halfhuf 99
<<<halfhuf 249
	there is 1 branch - process
>>>halfhuf 0..1 (6)- split
offset 6 - 0..0,1..1
	single 0 branch - literal 1 0x58 (X) 10|0
	single 1 branch - literal 0 0x56 (V) 11|1
<<<halfhuf 19
<<<halfhuf 269

что на 24 байта короче - выходит ELAINE02.WHI будет не 175 байт длиной, а уже 151, что даёт сжатие в 20.4 раза вместо озвученных выше 17.7 :o
Я тут за главного - если что шлите мыло на me собака shaos точка net
Top
User avatar
Shaos
Admin
Posts: 23763
Joined: 08 Jan 2003 23:22
Location: Silicon Valley

Re: Создаём подобие JPEG для ретрокомпов (Walsh+Huffman)

Post by Shaos »

Shaos wrote:(таблица Хаффмана в WHI смешивает в месте квантованные отсчёты и метки последовательностей нулей разной длины, представляя их как разные литералы)
Прикинул тут 2 варанта (ELAINE02 и ELAINE04) с RLE и без RLE и чото получается, что просто кодирование символов по частоте (голый Хаффман) даёт результаты лучше, чем Хаффман поверх RLE (когда нули собраны с спец.символы по количеству подряд идущих и замешаны с сэмплами в общем алфавите как в примерах выше) - наверное надо добавить как опцию возможность делать и так, и эдак (и потом в адаптивном алгоритме реализовать всё с выбором лучшего):

Code: Select all

11 - Huffman after RLE
10 - Huffman only
01 - RLE only
00 - Raw data
(последний вариант это голые квантованные данные чисто чтобы было)

Но отбрасывание хвостовых нулей я оставлю для всех вариантов т.к. их наличие уж точно ничего не даёт, а просто расходует попусту пространство (хотя с другой стороны, в случае отбрасывания нулей приходится заводить отдельный символ, означающий конец последовательности).

P.S. А пока выложил GRAPHIN на GitLab под MIT-лицензией вместе с одним примером и дополнительными классами BWS и BITIO (эти я выдаю как PUBLIC DOMAIN):

https://gitlab.com/shaos/graphin
Я тут за главного - если что шлите мыло на me собака shaos точка net
Top

Return to “Проект nedoPC”