Я решил тут потратить немного собственного времени и внести полную ясность и прозрачность
в конструктивные особенности АЛУ
К155ИП3 (
aka 74181) в финале топика об его "
странностях".
И мне лично все стало понятно в конструкции обсуждаемого АЛУ после
моего этого поста:
Lavr wrote:В источнике,
на который я ссылаюсь, принципы построения
АЛУ К155ИП3 объясняют
следующим образом:
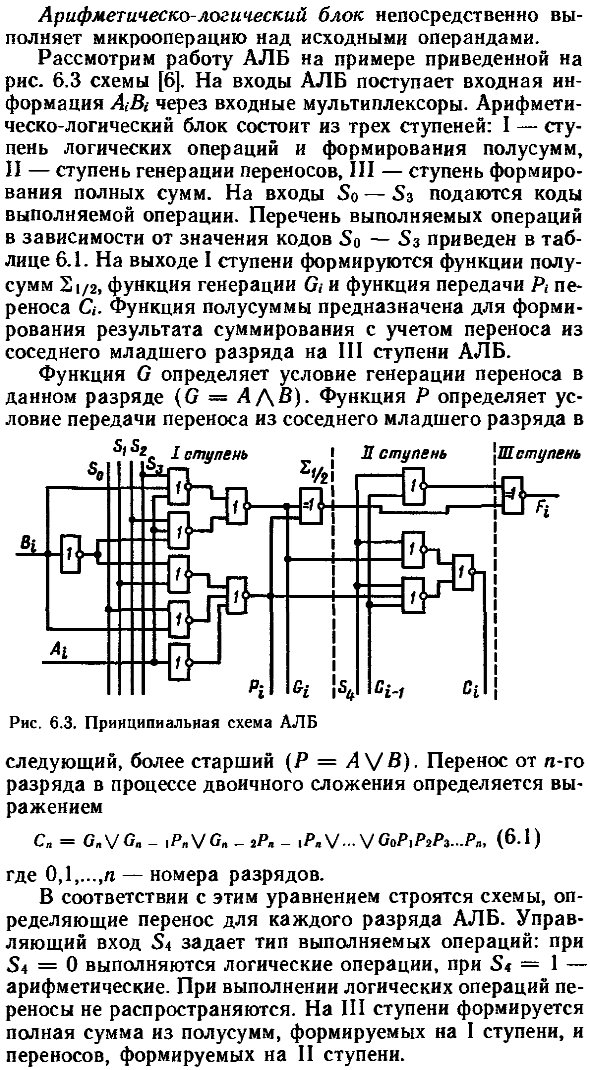
Но видимо не все читали приведенный там источник, и я с удивлением узнал, что и у меня
на работе не все четко понимают принцип работы этого АЛУ и путаются в его функциях.
Да и в книге, из которой скопирован материал, рассмотрен всего один каскад, что при взгляде
на остальные каскады вызывает некоторое замешательство - каскады на первый взгляд не похожи.
Поэтому я взял на себя труд нарисовать схему этого АЛУ, так чтобы при взгляде стал сразу
прозрачен принцип его работы, и любые функции можно было определить без таблиц.
Приведенные выше в топике схемы рисовали из принципа придать им компактный вид, поэтому
они сразу пугают своей якобы сложностью и запутанность. Я место на рисунке не экономил,
поэтому он получился довольно крупный, но, на мой взгляд, теперь совершенно понятный.
Хотя придется его скрыть под спойлер...
 Схема электрическая принципиальная ИС АЛУ К155ИП3(74181)
Схема электрическая принципиальная ИС АЛУ К155ИП3(74181): во входном каскаде
из входных аргументов A и B создается через элементы
И и НЕ набор из 5 логических функций в каждом каскаде. Эти функции или их комбинации с помощью
управляющих сигналов S0, S1, S2, S3 подают на входы первого каскада сумматора, выполненного
в этом АЛУ по совершенно традиционной схеме:
Full_Adder.gif
И вот тут обычно начинается путаница и недопонимание...
По этой схеме в АЛУ выполнен только каскад для сигналов
A0 и
B0, остальные каскады сделаны
на вид несколько иначе. И дело в том, что в этом АЛУ применен ускоренный параллельный перенос
для всех 4-х сумматоров одновременно. Это и делает схему АЛУ такой громоздкой.
Смысл параллельного переноса в том, что для каждого более старшего разряд сумматора логикой
выбираются ВСЕ комбинациии ВХОДНЫХ сигналов сумматоров младших разрядов, при которых у ЭТОГО
разряда сумматора должен произойти перенос. Поэтому с каждым разрядом схема параллельного
переноса становится "толще" и "толще" - надо учесть всё большее количество входных сигналов.
В этом плане построение сумматора с параллельным переносом похоже на построение многоразрядного
синхронного счетчика: он реально счетчиком-то в привычном смысле и не является, а представляет
собой параллельный регистр, в каждый триггер которого одновременно записываются комбинации
сигналов предыдуших разядов, а логика отслеживает, когда надо записать "
0",
а когда - "
1".
Следующий момент, который многих сбивает с толку:
АЛУ одинаково хорошо работает как со входными
сигналами, так и с их инверсиями, поэтому возникает путаница: в
одних справочниках приводят две таблицы для прямых входных сигналов и для их инверсий,
в других считают, что пользователи знакомы по меньшей мере с
законами дуальности де Моргана: это используется в схемотехнике АЛУ.
Если у булевой функции инвертировать входные сигналы и выходные сигналы, то она превращается
в двойственную ей функцию -
И в
ИЛИ,
ИЛИ в
И и т.п.
Но, думаю, не все знают, что
полный сумматор - самодвойственная булева функция:
при инверсии
входных сигналов сумматор инвертирует выходные сигналы, но остается сумматором.
То есть, сумматор одинаково хорошо суммирует как прямые значения на входах, так и их инверсии,
но во втором случае он инвертирует сигналы у себя на выходе.
Значит, если вместо
A и
B мы подадим на входы сумматора
/A и
/B он вычислит вместо
S ---
/S.
Теперь о логических функциях АЛУ: следует помнить, что
XOR - в общем-то тоже вентиль, который
является управляемым инвертором. И в одном из состояний - он повторитель входного сигнала.
В АЛУ это используют так: специальный
сигнал М запрещает подачу на
выходной XOR сумматоров
сформированные сигналы параллельных переносов, и
выходной XOR просто передает на выход АЛУ
какую-то логическую комбинацию из входного каскада. Эту комбинацию определяют управляющие
сигналы
S0, S1, S2, S3.
На своей схеме я нарисовал все функции для прямых сигналов
A и
B. Для инверсных сигналов
/A и
/B наборы логических сигналов, согласно законам дуальности де Моргана, будут другие.
Но так и выбрать нужные следует другими комбинациями управляющих сигналов
S0, S1, S2, S3
И если никто не забыл
основные аксиомы и тождества булевой алгебры-логики, то всё нужное
вырисовывается просто элементарно!
P.S. И я подумал - краткую шпаргалку основных аксиом и тождеств булевой алгебры-логики здесь тоже неплохо приложить: 
 Аксиомы и тождества булевой алгебры-логики
Аксиомы и тождества булевой алгебры-логикиYou do not have the required permissions to view the files attached to this post.



